| Issue |
Med Sci (Paris)
Volume 31, Number 10, Octobre 2015
|
|
|---|---|---|
| Page(s) | 889 - 894 | |
| Section | M/S Revues | |
| DOI | https://doi.org/10.1051/medsci/20153110015 | |
| Published online | 19 October 2015 | |
Hasard et destinée cellulaire
Randomness and cell fate
École supérieure de physique et chimie industrielle (ESPCI), laboratoire de biochimie, 10, rue Vauquelin, 75005 Paris, France
Les fluctuations thermiques à l’échelle moléculaire génèrent des fluctuations aléatoires d’expression des gènes, qui, lorsqu’elles sont associées à des circuits de différenciation, donnent lieu à une diversification phénotypique à l’échelle de populations de cellules. Dans cette synthèse, nous détaillerons les mécanismes moléculaires à l’origine de cette diversification et illustrerons leurs conséquences dans différents organismes. Chez les bactéries, la diversification phénotypique aléatoire permet d’anticiper des changements de l’environnement, autrement imprévisibles, en particulier d’optimiser les transitions métaboliques et la réponse au stress, induisant par exemple une forme transitoire de résistance aux traitements antibiotiques. Dans les organismes pluricellulaires, des mécanismes similaires permettent la maintenance des tissus sains, tels que les intestins, l’épiderme ou la rétine, mais semblent également jouer un rôle dans l’établissement et la maintenance de l’hétérogénéité tumorale.
Abstract
Thermal fluctuations at the molecular scale cause random fluctuations of gene expression, which, in association with differentiation circuits, can lead to phenotypic diversification in cell populations. In this synthesis article, we detail the mechanisms that generate this diversification and illustrate their consequences in various organisms. In bacteria, random phenotypic diversification allows to anticipate environmental changes that are otherwise unpredictable, in particular during metabolic transitions and stress responses, for example inducing a transient form of antibiotic resistance. In multi-cellular organisms, similar mechanisms allow the maintenance of healthy tissues, such as intestinal crypts, epidermis and retina, but also seem to play a role in establishment and renewal of tumoral heterogeneity.
© 2015 médecine/sciences – Inserm
Les cellules sont perpétuellement soumises à des mutations ou à des modifications environnementales susceptibles de modifier leur état. Des travaux à la frontière de la biophysique et de la biologie cellulaire, ont établi, depuis une quinzaine d’années, l’importance d’une source de perturbations différente, liée au caractère stochastique des réactions biochimiques. On sait en effet depuis la fin du XIXe siècle que l’agitation thermique affecte de manière significative les processus à l’échelle moléculaire. Elle permet aux molécules de diffuser pour réagir entre elles. Ces processus sont traditionnellement modélisés par des équations cinétiques continues (par exemple l’équation de Michaelis-Menten). Ce type de modèle, couramment utilisé pour les réactions intracellulaires, n’est justifié que lorsqu’un nombre élevé de molécules est en jeu. En effet, en probabilité, la « loi des grands nombres » indique que la variance d’un processus, répété indépendamment N fois, est de l’ordre N, si bien que l’amplitude des fluctuations (représentée par l’écart-type) rapportée à la moyenne diminue comme la racine carré de N, ce qui donne, par exemple, une fluctuation de 1 % lorsque 10 000 molécules sont en jeu. Force est de constater que de nombreux objets biologiques se comptent en petit nombre par cellule, à commencer par les gènes qui sont généralement présents en une seule copie et transcrits par dizaines chez les bactéries, et par centaines chez les eucaryotes. Ainsi, la loi statistique énoncée ci-dessus, donne lieu à une variabilité relative de 30 % pour N = 10 transcrits. Comme nous le verrons, bien que ce modèle soit extrêmement simplifié, le résultat correspond bien à la variabilité du niveau d’expression génétique qui est mesuré en général.
Cette variabilité se maintient-elle au niveau de l’expression des protéines qui sont, elles, exprimées par milliers ? Peut-elle avoir des conséquences physiologiques à l’échelle de la cellule, des tissus, voire des organismes entiers ? Ces questions ont été abordées expérimentalement à l’échelle de la cellule unique par des mesures quantitatives essentiellement basées sur la microscopie de fluorescence et le traitement d’image automatisé. Nous examinerons comment les fluctuations thermiques, associées aux différents processus moléculaires, génèrent des fluctuations aléatoires, ou bruit, dans l’expression génétique. Nous verrons également comment ce bruit se transmet à travers les réactions intracellulaires. Lorsqu’il est associé à des architectures génétiques programmant des états cellulaires multiples, ce bruit génère de la diversité phénotypique dans les populations de cellules. Cela peut, d’une part, provoquer une résistance aux conditions adverses, en particulier aux traitements, et, d’autre part, conduire à l’établissement de proportions contrôlées entre plusieurs types cellulaires. Nous illustrerons ces propriétés dans le cas des microbes, puis dans le cadre d’organismes multicellulaires, pour la maintenance de tissus et l’hétérogénéité de tumeurs cancéreuses.
Les origines du bruit dans l’expression génétique
La première démonstration systématique de bruit dans l’expression génétique a été rapportée chez la bactérie Escherichia coli [1]. Ceci a été réalisé en exprimant deux protéines fluorescentes, contrôlées par un promoteur identique, les gènes étant introduits de manière parfaitement symétrique sur le chromosome afin de supprimer toute source de variabilité autre que les fluctuations locales d’expression génétique (Figure 1A). Les auteurs ont observé une variabilité, entre les cellules, de l’expression relative des deux gènes introduits (Figure 1B), variabilité d’autant plus grande (entre 10 % et 50 %) que le nombre moyen de protéines exprimé est faible. Cette tendance est en parfait accord avec les lois statistiques (telles que celle énoncée dans l’introduction) décrivant la dynamique d’expression génétique par des événements de production aléatoire de transcrits. Ces mesures ont été ensuite reproduites dans les levures [2], organismes eucaryotes, démontrant qu’il ne s’agissait pas d’une spécificité des procaryotes. Ces conclusions ont été rapidement étoffées par comptage de molécules uniques au sein de cellules uniques [3], révélant que durant les phases d’activation du promoteur, les ARN sont transcrits de manière aléatoire sous la forme de « bouffées » (Figure 1C).
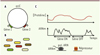 |
Figure 1. Origine du bruit d’expression génétique. A. Construction symétrique de gènes exprimant deux protéines fluorescentes distinctes, mais contrôlées par le même promoteur et équidistants de l’origine de réplication, de manière à supprimer les fluctuations liées au cycle cellulaire. B. La proportion relative des fluorescences varie de manière différentielle dans le temps et entre bactéries au sein d’une colonie clonale, indiquant l’existence de fluctuations locales d’expression au niveau de chaque gène. C. L’expression des ARN a lieu par bouffées lorsque le promoteur est actif. La concentration de protéines suit ces fluctuations, cependant de manière plus douce, en raison de la dilution due à la croissance qui introduit un temps de relaxation des variations de l’ordre du cycle cellulaire. |
Une fois établie l’existence de sources de bruit, se pose la question de sa transmission à travers les réseaux d’interactions génétiques et de réactions enzymatiques. Deux hypothèses s’opposent : soit l’accumulation de processus aléatoires s’annule par un effet de moyenne (scénario 1), soit le caractère hautement coopératif et spécifique des processus biologiques conduit à une amplification du bruit (scénario 2). Pour répondre à cette question, des constructions génétiques synthétiques ont été introduites dans des bactéries de manière à suivre les fluctuations d’expression de plusieurs gènes se régulant mutuellement [4]. Les auteurs ont ainsi pu montrer que les amplitudes des fluctuations tendent à s’ajouter les unes aux autres, à travers une cascade de régulation, conformément au scénario 2. Si cette expérience apporte une preuve de principe, on peut se demander jusqu’à quel point les conclusions que l’on en tire sont applicables à des réseaux génétiques naturels.
Des mesures de fluctuations ont pu être réalisées de manière hautement parallélisée sur des milliers de gènes bactériens, in vivo, par microscopie de fluorescence effectuée dans des chambres microfluidiques [5]. Dans ces conditions, on observe que l’amplitude des fluctuations d’expression des gènes diminue lorsque ceux-ci sont exprimés à un niveau plus élevé, comme on le prédirait par un effet de moyenne. Mais, de manière plus surprenante, il apparaît un niveau de bruit plancher, de l’ordre de 30 %, valable pour les ARN exprimés d’une dizaine à plusieurs milliers de copies. Un examen de la coexpression de multiples paires de gènes résout en partie ce mystère, en indiquant l’existence d’une hiérarchie de facteurs de bruit communs. Certains affectent uniquement des paires de gènes données, par exemple lorsque ces derniers sont régulés par un même facteur de transcription, d’autres sont des sources de bruit globales affectant l’ensemble des gènes, telles que discutées ci-après.
Le métabolisme génère les ressources élémentaires communes à tous les processus de polymérisation des molécules biologiques. Bien que les métabolites soient présents en très grand nombre, leur flux résulte de l’activité d’enzymes qui sont exprimées de manière fluctuante. Le suivi de la croissance de cellules uniques, en conjonction avec le niveau d’expression d’enzymes cataboliques, montre ainsi que le bruit des enzymes limitantes se transmet à travers le métabolisme et affecte la croissance de manière significative [6, 7]. Il semble, par ailleurs, que le bruit global soit proportionnel à la concentration des polymérases ARN [8], représentant une autre source potentielle de bruit global. D’autres facteurs sont potentiellement à l’origine de ce bruit, tels que les ribosomes ou encore la structure du chromosome au cours du cycle cellulaire, mais la question reste non élucidée.
Une difficulté conceptuelle et pratique réside dans le caractère bouclé du système, les sources de bruit global entretenant nécessairement les fluctuations de processus moléculaires à leur propre origine. Des outils théoriques se développent pour décomposer le bruit en sources multiples, dans des réseaux de plus en plus complexes [9, 10]. Ils devraient permettre de concevoir des expériences quantifiant leur importance relative. Bien qu’il reste de nombreuses questions fondamentales à résoudre, nos connaissances sur le bruit d’expression génétique permettent d’ores et déjà d’aborder de nombreux phénomènes d’importance physiologique.
Diversification phénotypique chez les microbes
Nous avons vu comment des fluctuations aléatoires d’expression génétique sont inévitablement générées dans chaque cellule. Ces cellules peuvent, de fait, les exploiter pour diversifier leur état de manière durable. Il suffit pour cela d’associer le bruit d’un gène à un processus décisionnel conduisant, à un moment donné, à la stabilisation dans un état ou un autre, en fonction d’un seuil comme dans un jeu de pile ou face (Figure 2A). Ce mécanisme a été démontré pour la première fois dans un modèle non cellulaire, celui du phage lambda, virus infectant les bactéries, dont le caractère aléatoire a été étudié dès 1945 [11]. Ainsi, un module génétique de deux répresseurs s’inhibant l’un l’autre, donne lieu à deux états stables mutuellement exclusifs. C’est la susceptibilité de ce module aux fluctuations d’expression qui contrôle le taux de transition vers l’état lytique du phage, conduisant à l’explosion de la bactérie qu’il a infectée et la propagation du virus [12].
 |
Figure 2. Diversification phénotypique aléatoire. A. Dans le scénario illustré ici, un facteur environnemental déclenche une inhibition mutuelle, conduisant à une transition de un à deux états stables du système, délimités par un certain niveau seuil d’expression du gène 1. Avant l’introduction du facteur environnemental, les fluctuations d’expression du gène 1 sont uni-modales. Après l’introduction du facteur, les fluctuations sont confinées au-dessus ou en-dessous du seuil et deviennent bimodales, la probabilité d’appartenir à un état ou l’autre étant fonction des fluctuations antérieures et de la valeur du seuil. B. Les bactéries expriment de manière aléatoire le programme de réponse au stress, ce qui permet à la fraction correspondante de la population de survivre lors de l’introduction brutale d’antibiotiques dans le milieu. À la fin du traitement, ces individus reviennent aléatoirement à un état non stressé, permettant à nouveau la division et l’établissement d’une nouvelle colonie. |
Si être imprévisible représente un avantage évident pour un pathogène, diversifier son état s’avère utile de façon générale, pour répondre à des signaux externes, qu’ils proviennent d’autres cellules ou qu’ils soient le fait d’un environnement fluctuant. Une stratégie de diversification aléatoire est par nature collective et se justifie dans le cadre de populations clonales de microbes ayant développé un panel de phénotypes appropriés au cours de l’évolution. Une stratégie alternative est la détection spécifique de stimulus externes qui déclenchent une réponse génétiquement programmée. Il a été prédit en théorie, que la stratégie aléatoire devient avantageuse lorsque les changements environnementaux sont relativement peu fréquents, auquel cas un module génétique serait trop peu utilisé par rapport aux ressources qu’il consomme [13]. On peut toutefois nuancer cette prédiction en remarquant que les processus décisionnels aléatoires mettent eux aussi en jeu des structures génétiques spécifiques, permettant de fixer des phénotypes particuliers, la bistabilité nécessitant, par exemple, des boucles de rétroaction positives et/ou des inhibitions mutuelles entre gènes, comme illustré ci-dessous.
Les bactéries entériques sont confrontées à des changements brutaux de ressources nutritionnelles, étant confrontées cycliquement au système digestif et à l’environnement extérieur. Elles disposent de régulations génétiques comme l’opéron lactose, leur permettant d’exprimer les enzymes appropriées en fonction de la source de carbone disponible qu’elles rencontrent. Il a été observé chez E. coli [14, 15] et Lactococcus lactis [16] qu’une fraction des cellules était capable de répondre de manière quasi-instantanée durant la diauxie, c’est-à-dire la transition entre le métabolisme de différents sucres. Cette réponse est beaucoup plus rapide que la réponse moyenne de la population qui, elle, montre une phase dite de « lag » de plusieurs dizaines de minutes. Cette réponse immédiate est de fait déclenchée par l’expression précoce et aléatoire de gènes normalement réprimés par une fraction de la population. Il ne s’agit là finalement que d’une réinterprétation plus quantitative de la bistabilité de l’opéron lactose, constatée dès les débuts de la biologie moléculaire [17]. La cellule reste de fait aveugle au lactose extracellulaire tant qu’un événement aléatoire n’a pas amorcé la production de pompes (LacY)1 important le lactose (mesuré cette fois, de manière intracellulaire), en induisant un changement de conformation de la protéine lacI, régulateur de l’expression des enzymes.
Les bactéries possèdent également des mécanismes génériques de réponse au stress, déclenchés, entre autres, par l’absence de nourriture ou des changements osmotiques. Dans le cas de Bacillus subtilis, le programme de réponse au stress est contrôlé par le facteur de transcription σB. Il a été montré que lorsque le niveau de stress augmente, une rétroaction positive entre les trois gènes associés à l’opéron codant σB devient de plus en plus excitable en réponse au bruit d’expression génétique, conduisant à une activation d’autant plus fréquente des gènes associés [18].
La diversification phénotypique aléatoire joue un rôle prépondérant dans la réponse aux antibiotiques (Figure 2B). L’observation de cellules uniques soumises à des antibiotiques pendant une fenêtre de temps montre l’existence d’une petite fraction de bactéries, dites persistantes, capables de se diviser à nouveau et de donner de nouvelles colonies lorsque le traitement est interrompu, alors que la grande majorité des bactéries meurt [19]. Contrairement aux bactéries résistantes, les bactéries persistantes n’ont pas acquis de mutation. Elles correspondent à une sous-population qui exprime, par hasard, le programme de réponse au stress dans un environnement initialement non stressant. Bien qu’à l’origine ces bactéries représentent un coût pour la colonie, se divisant à peine en milieu riche, ce préjudice est compensé par un bénéfice extrêmement grand en présence d’antibiotiques. Encore une fois, la possibilité d’une telle stratégie semble correspondre à l’existence de plusieurs états de croissance stables [20].
Homéostasie des tissus sains et tumoraux
Les mécanismes de diversification phénotypique décrits dans le cas des microbes sont en cours de caractérisation chez les organismes multicellulaires. Ils semblent suivre des principes très similaires. En particulier, l’association entre facteurs stochastiques et processus décisionnels émerge comme un modèle générique de maintenance des organes [21]. L’idée est de modéliser la dynamique de différenciation, comme un processus de transitions aléatoires entre les états accessibles. Lorsque les probabilités de ces transitions sont fixées, on peut démontrer mathématiquement qu’une telle dynamique, dite chaîne de Markov, converge vers une proportion, bien déterminée et stable, des différents états et ce, pour une grande variété de conditions initiales. Ainsi, cette stratégie présente une forme de robustesse en permettant de ré-établir une population stable à partir d’une grande diversité d’états.
L’existence de facteurs aléatoires dans les processus de différenciation a été suggérée dans les cellules hématopoïétiques dès le milieu des années 1990 [22]. Ceci a été confirmé par des expériences d’établissements successifs de populations, à partir d’une cellule unique isolée. Ces populations présentent systématiquement la même variabilité d’expression génétique [23]. La dynamique d’établissement de ces distributions d’états génétiques suggère notamment l’existence d’états métastables (temporairement stables) sous-jacents, par lesquels le système doit transiter avant d’atteindre un état définitivement stable. Une démonstration plus directe d’une dynamique de transitions aléatoires entre états multiples, et suivant des taux fixes, a ensuite été obtenue par le suivi de lignées fluorescentes de cellules de rétine de rat [24], associé aux états de différenciation, en fonction de leur morphologie et leur mobilité.
En parallèle, la validité de ce type de dynamique a pu être établie in vivo, avec en premier lieu, les cryptes intestinales [25]. Lopez-Garcia et al. ont mesuré dans des coupes intestinales de souris, la dynamique d’envahissement des cryptes par une petite fraction de cellules marquées. Ils ont pu démontrer que le renouvellement de ces cryptes ne respectait pas le modèle hiérarchique proposé classiquement, dans lequel une cellule souche permanente, logée au fond de chaque crypte, régénère le tissu environnant de manière déterministe, mais plutôt qu’il suivait une dynamique de transitions aléatoires entre un état prolifératif et un état différencié (Figure 3). Une étude similaire de l’épiderme de souris montre une dynamique plus hiérarchique, entre un type prolifératif et un type différencié, mais toujours suivant des règles de transitions aléatoires [26]. Ainsi, si les processus de transitions aléatoires semblent être répandus (également observés pour les cellules souches pluripotentes [27] et les cellules immunitaires [28]), les architectures génétiques sous-jacentes semblent très diverses.
 |
Figure 3. Régénération des cryptes intestinales. A. Dans un modèle exclusivement hiérarchique, une cellule souche unique (bleue) est seule capable de se diviser, ce qu’elle fait de manière systématiquement asymétrique en donnant une cellule fille différenciée (jaune), évoluant ensuite vers d’autres types au cours de sa maturation (vert). B. Dans ce modèle, la cellule souche est à la base de la crypte et les types différenciés migrent progressivement jusqu’au lumen. C. Lopez-Garcia et al. ont montré que les cellules souches suivent au contraire deux options suivant une dynamique globale aléatoire : soit elles se divisent de manière symétrique, donnant deux cellules souches, soit elles se différencient. D. Le fond des cryptes est donc constitué d’un groupe de cellules souches capables de se substituer mutuellement lors de leurs divisions, les nouvelles cellules souches remplaçant celles qui se différencient et remontent la crypte. |
Enfin, il a été suggéré récemment que le bruit d’expression génétique et la diversification phénotypique jouent un rôle clé dans l’évolution des tumeurs [29]. Il a été démontré que les cellules extraites de tumeurs du sein sont non seulement hétérogènes, mais que cette hétérogénéité peut s’expliquer par un schéma de taux de transitions fixes entre tous les types observés [30]. En effet, Gupta et al. ont pu ré-établir in vitro des tumeurs d’hétérogénéité identique à partir de n’importe lequel des types différenciés. Comme dans le cas de la maintenance des tissus sains, le modèle hiérarchique déterministe et coordonné fait place à une dynamique d’interconversion aléatoire entre états. Une conclusion identique a également été obtenue par transplantation in vivo de cellules cancéreuses de peau [31]. Ici encore, la question de la hiérarchie entre phénotypes cellulaires reste pleinement ouverte, et suggère d’élargir l’hypothèse de cellules souches cancéreuses, en incluant la possibilité d’interconversions entre types cellulaires multiples.
Conclusion
Les fluctuations thermiques à l’échelle moléculaire génèrent des fluctuations aléatoires d’expression des gènes, qui se transmettent aux autres gènes à travers les réseaux d’interactions cellulaires. Lorsque ce bruit d’expression génétique est associé à des circuits de différenciation, il donne lieu à une dynamique de diversification phénotypique à l’échelle de populations de cellules. Il est remarquable qu’un processus basé sur le hasard permette de maintenir une proportion robuste et bien définie de chaque type cellulaire, et ce par un programme de décisions individuelles, sans faire nécessairement intervenir de communication entre cellules. Ce paradoxe apparent disparaît à l’échelle collective, puisqu’un programme probabiliste mais identique pour chaque cellule, conduit à un état statistiquement stable à l’échelle de la population.
Chez les microbes, le lien entre architecture génétique de différenciation et bruit d’expression implique généralement des rétroactions positives et des inhibitions mutuelles. La diversification phénotypique résultante permet de répondre rapidement à des changements environnementaux imprévisibles et potentiellement stressants, avec pour conséquence notable la survie d’une fraction de bactéries, dites persistantes, aux traitements antibiotiques.
Dans les organismes pluricellulaires, des mécanismes similaires permettent la maintenance des tissus tels que les intestins, l’épiderme ou la rétine. Bien que les circuits génétiques de différenciation soient de mieux en mieux cartographiés et le bruit d’expression génétique caractérisé, leurs liens précis restent à démontrer. Il semble que les dynamiques de diversifications aléatoires jouent également un rôle dans l’établissement de l’hétérogénéité tumorale. Des études récentes montrent que cette hétérogénéité aléatoire peut générer des résistances aux traitements d’une fraction des cellules cancéreuses [32], s’ajoutant à l’hétérogénéité génétique, à l’instar du scénario de persistance observé chez les bactéries.
Enfin, la programmation générique et la relative simplicité de ces scénarios de diversification aléatoire ouvrent des perspectives évolutives fascinantes concernant la transition vers la pluricellularité.
Liens d’intérêt
L’auteur déclare n’avoir aucun lien d’intérêt concernant les données publiées dans cet article.
Références
- Elowitz MB, Levine AJ, Siggia ED, et al. Stochastic gene expression in a single cell. Science 2002 ; 297 : 1183–1186. [CrossRef] [PubMed] [Google Scholar]
- Raser JM, O’Shea EK. Control of stochasticity in eukaryotic gene expression. Science 2004 ; 304 : 1811–1814. [CrossRef] [PubMed] [Google Scholar]
- Cai L, Friedman N, Xie XS. Stochastic protein expression in individual cells at the single molecule level. Nature 2006 ; 440 : 358–362. [CrossRef] [PubMed] [Google Scholar]
- Pedraza JM, van Oudenaarden A. Noise propagation in gene networks. Science 2005 ; 307 : 1965–1969. [CrossRef] [PubMed] [Google Scholar]
- Taniguchi Y, Choi PJ, Li GW, et al. Quantifying E. coli proteome and transcriptome with single-molecule sensitivity in single cells. Science 2010 ; 329 : 533–538. [CrossRef] [PubMed] [Google Scholar]
- Kiviet DJ, Nghe P, Walker N, et al. Stochasticity of metabolism and growth at the single-cell level. Nature 2014 ; 514 : 376–379. [CrossRef] [PubMed] [Google Scholar]
- Nghe P, Boulineau S, Tans SJ. Fluctuations aléatoires dans le métabolisme et la croissance cellulaires. Med Sci (Paris) 2015 ; 31 : 233–235. [CrossRef] [EDP Sciences] [PubMed] [Google Scholar]
- Yang S, Kim S, Lim YR, et al. Contribution of RNA polymerase concentration variation to protein expression noise. Nat Commun 2014 ; 5 : 4761. [CrossRef] [PubMed] [Google Scholar]
- Dunlop MJ, Cox RS, Levine JH, et al. Regulatory activity revealed by dynamic correlations in gene expression noise. Nat Genet 2008 ; 40 : 1493–1498. [CrossRef] [PubMed] [Google Scholar]
- Bowsher CG, Swain PS. Identifying sources of variation and the flow of information in biochemical networks. Proc Natl Acad Sci USA 2012 ; 109 : 1320–1328. [Google Scholar]
- Delbrück M.. The burst size distribution in the growth of bacterial viruses (bacteriophages). J Bacteriol 1945 ; 50 : 131. [Google Scholar]
- Arkin A, Ross J, McAdams HH. Stochastic kinetic analysis of developmental pathway bifurcation in phage λ-infected Escherichia coli cells. Genetics 1998 ; 149 : 1633–1648. [PubMed] [Google Scholar]
- Kussell E, Leibler S. Phenotypic diversity, population growth, and information in fluctuating environments. Science 2005 ; 309 : 2075–2078. [CrossRef] [PubMed] [Google Scholar]
- Boulineau S, Tostevin F, Kiviet DJ, et al. Single-cell dynamics reveals sustained growth during diauxic shifts. PLoS One 2013 ; 8 : e61686. [CrossRef] [PubMed] [Google Scholar]
- Robert L, Paul G, Chen Y, et al. Pre-dispositions and epigenetic inheritance in the Escherichia coli lactose operon bistable switch. Mol Syst Biol 2010 ; 6 : 357. [CrossRef] [PubMed] [Google Scholar]
- Solopova A, van Gestel J, Weissing FJ, et al. Bet-hedging during bacterial diauxic shift. Proc Natl Acad Sci USA 2014 ; 111 : 7427–7432. [CrossRef] [Google Scholar]
- Novick A, Weiner M. Enzyme induction as an all-or-none phenomenon. Proc Natl Acad Sci USA 1957 ; 43 : 553–566. [CrossRef] [Google Scholar]
- Locke JC, Young JW, Fontes M, et al. Stochastic pulse regulation in bacterial stress response. Science 2011 ; 334 : 366–369. [CrossRef] [PubMed] [Google Scholar]
- Balaban NQ, Merrin J, Chait R, et al. Bacterial persistence as a phenotypic switch. Science 2004 ; 305 : 1622–1625. [CrossRef] [PubMed] [Google Scholar]
- Deris JB, Kim M, Zhang Z, et al. The innate growth bistability and fitness landscapes of antibiotic-resistant bacteria. Science 2013 ; 342 : 1237435. [CrossRef] [PubMed] [Google Scholar]
- Simons BD, Clevers H. Strategies for homeostatic stem cell self-renewal in adult tissues. Cell 2011 ; 145 : 851–862. [CrossRef] [PubMed] [Google Scholar]
- Abkowitz JL, Catlin SN, Guttorp P. Evidence that hematopoiesis may be a stochastic process in vivo. Nat Med 1996 ; 2 : 190–197. [CrossRef] [PubMed] [Google Scholar]
- Chang HH, Hemberg M, Barahona M, et al. Transcriptome-wide noise controls lineage choice in mammalian progenitor cells. Nature 2008 ; 453 : 544–547. [CrossRef] [PubMed] [Google Scholar]
- Gomes FL, Zhang G, Carbonell F, et al. Reconstruction of rat retinal progenitor cell lineages in vitro reveals a surprising degree of stochasticity in cell fate decisions. Development 2011 ; 138 : 227–235. [CrossRef] [PubMed] [Google Scholar]
- Lopez-Garcia C, Klein AM, Simons BD, et al. Intestinal stem cell replacement follows a pattern of neutral drift. Science 2010 ; 330 : 822–825. [CrossRef] [PubMed] [Google Scholar]
- Mascré G, Dekoninck S, Drogat B, et al. Distinct contribution of stem and progenitor cells to epidermal maintenance. Nature 2012 ; 489 : 257–262. [CrossRef] [PubMed] [Google Scholar]
- Buganim Y, Faddah DA, Cheng AW, et al. Single-cell expression analyses during cellular reprogramming reveal an early stochastic and a late hierarchic phase. Cell 2012 ; 150 : 1209–1222. [CrossRef] [PubMed] [Google Scholar]
- Fang M, Xie H, Dougan SK, et al. Stochastic cytokine expression induces mixed T helper cell states. PLoS Biol 2013 ; 11 : e1001618. [CrossRef] [PubMed] [Google Scholar]
- Brock A, Chang H, Huang S. Non-genetic heterogeneity: a mutation-independent driving force for the somatic evolution of tumours. Nat Rev Genet 2009 ; 10 : 336–342. [Google Scholar]
- Gupta PB, Fillmore CM, Jiang G, et al. Stochastic state transitions give rise to phenotypic equilibrium in populations of cancer cells. Cell 2011 ; 146 : 633–644. [CrossRef] [PubMed] [Google Scholar]
- Driessens G, Beck B, Caauwe A, et al. Defining the mode of tumour growth by clonal analysis. Nature 2012 ; 488 : 527–530. [CrossRef] [PubMed] [Google Scholar]
- Roux J, Hafner M, Bandara S, et al. Fractional killing arises from cell-to-cell variability in overcoming a caspase activity threshold. Mol Syst Biol 2015 ; 11 : 803. [CrossRef] [PubMed] [Google Scholar]
Liste des figures
 |
Figure 1. Origine du bruit d’expression génétique. A. Construction symétrique de gènes exprimant deux protéines fluorescentes distinctes, mais contrôlées par le même promoteur et équidistants de l’origine de réplication, de manière à supprimer les fluctuations liées au cycle cellulaire. B. La proportion relative des fluorescences varie de manière différentielle dans le temps et entre bactéries au sein d’une colonie clonale, indiquant l’existence de fluctuations locales d’expression au niveau de chaque gène. C. L’expression des ARN a lieu par bouffées lorsque le promoteur est actif. La concentration de protéines suit ces fluctuations, cependant de manière plus douce, en raison de la dilution due à la croissance qui introduit un temps de relaxation des variations de l’ordre du cycle cellulaire. |
| Dans le texte | |
 |
Figure 2. Diversification phénotypique aléatoire. A. Dans le scénario illustré ici, un facteur environnemental déclenche une inhibition mutuelle, conduisant à une transition de un à deux états stables du système, délimités par un certain niveau seuil d’expression du gène 1. Avant l’introduction du facteur environnemental, les fluctuations d’expression du gène 1 sont uni-modales. Après l’introduction du facteur, les fluctuations sont confinées au-dessus ou en-dessous du seuil et deviennent bimodales, la probabilité d’appartenir à un état ou l’autre étant fonction des fluctuations antérieures et de la valeur du seuil. B. Les bactéries expriment de manière aléatoire le programme de réponse au stress, ce qui permet à la fraction correspondante de la population de survivre lors de l’introduction brutale d’antibiotiques dans le milieu. À la fin du traitement, ces individus reviennent aléatoirement à un état non stressé, permettant à nouveau la division et l’établissement d’une nouvelle colonie. |
| Dans le texte | |
 |
Figure 3. Régénération des cryptes intestinales. A. Dans un modèle exclusivement hiérarchique, une cellule souche unique (bleue) est seule capable de se diviser, ce qu’elle fait de manière systématiquement asymétrique en donnant une cellule fille différenciée (jaune), évoluant ensuite vers d’autres types au cours de sa maturation (vert). B. Dans ce modèle, la cellule souche est à la base de la crypte et les types différenciés migrent progressivement jusqu’au lumen. C. Lopez-Garcia et al. ont montré que les cellules souches suivent au contraire deux options suivant une dynamique globale aléatoire : soit elles se divisent de manière symétrique, donnant deux cellules souches, soit elles se différencient. D. Le fond des cryptes est donc constitué d’un groupe de cellules souches capables de se substituer mutuellement lors de leurs divisions, les nouvelles cellules souches remplaçant celles qui se différencient et remontent la crypte. |
| Dans le texte | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




