| Numéro |
Med Sci (Paris)
Volume 26, Numéro 1, Janvier 2010
|
|
|---|---|---|
| Page(s) | 49 - 56 | |
| Section | Biologie des systèmes | |
| DOI | https://doi.org/10.1051/medsci/201026149 | |
| Publié en ligne | 15 janvier 2010 | |
Biologie des systèmes et rythmes cellulaires
Circadian rhythms and systems biology
Unité de chronobiologie théorique, Faculté des sciences, Université Libre de Bruxelles, Campus Plaine, CP 231, B-1050 Bruxelles, Belgique
Les rythmes cellulaires representent un domaine d’investigation de choix pour la biologie des systemes. Les exemples des rythmes circadiens et du cycle cellulaire montrent comment l’experience et la modelisation permettent de clarifier les conditions dans lesquelles les comportements periodiques surviennent de maniere spontanee au sein des reseaux de regulation cellulaire. Les rythmes circadiens resultent de boucles de retroactions positives et negatives controlant l’expression de genes de l’horloge. Le cycle cellulaire repose sur de multiples regulations entrecroisees au sein d’un reseau de kinases dependantes de cyclines. Dans les deux cas, comme pour d’autres rythmes cellulaires decrits au cours des annees recentes, le comportement periodique represente une propriete emergente des systemes biologiques liee a leurs regulations.
Abstract
Cellular rhythms represent a field of choice for studies in system biology. The examples of circadian rhythms and of the cell cycle show how the experimental and modeling approaches contribute to clarify the conditions in which periodic behavior spontaneously arises in regulatory networks at the cellular level. Circadian rhythms originate from intertwined positive and negative feedback loops controlling the expression of several clock genes. Models can be used to address the dynamical bases of physiological disorders related to dysfunctions of the mammalian circadian clock. The cell cycle is driven by a network of cyclin-dependent kinases (Cdks). Modeled in the form of four modules coupled through multiple regulatory interactions, the Cdk network operates in an oscillatory manner in the presence of sufficient amounts of growth factor. For circadian rhythms and the cell cycle, as for other recently observed cellular rhythms, periodic behavior represents an emergent property of biological systems related to their regulatory structure.
© 2010 médecine/sciences - Inserm / SRMS
Les rythmes se rencontrent à tous les niveaux de l’organisation biologique, avec des périodes allant de la fraction de seconde à la dizaine d’années [1]. Nombre de ces rythmes surviennent déjà au niveau cellulaire, voire dans une cellule isolée (Tableau I). Ces comportements oscillants sont alors d’origine moléculaire : ils résultent de processus de régulation qui peuvent prendre de multiples formes. Ainsi les rythmes neuronaux et le rythme cardiaque reposent sur la régulation de canaux ioniques. Des oscillations biochimiques, dont l’exemple le mieux connu est celui des oscillations glycolytiques, sont dues au contrôle de l’activité enzymatique. La régulation de récepteurs, couplée à la régulation enzymatique, est à l’origine des oscillations du taux d’AMP cyclique chez l’amibe Dictyostelium, tandis que la régulation du transport entre différents compartiments cellulaires est responsable de celles du taux de calcium cytosolique. Enfin, le contrôle de l’expression de gènes sous-tend les rythmes circadiens, d’une période proche de 24 heures, et l’horloge de segmentation, d’une période de 30 minutes à 2 heures, impliquée dans la somitogenèse.
Principaux rythmes biologiques.
Biologie des systèmes : synergie entre expérience et modélisation
Résultant des processus de rétroaction au sein des systèmes biologiques, les rythmes fournissent un exemple emblématique de la biologie des systèmes. Ils représentent en effet une propriété émergente des réseaux de régulation (voir Encadré). Si les mécanismes qui sous-tendent la dynamique oscillante des systèmes biologiques demandent chaque fois à être mis à jour de manière expérimentale, la compréhension de cette dynamique bénéficie d’un recours à la modélisation mathématique. La modélisation du mécanisme d’un rythme biologique consiste à décrire par des équations cinétiques les changements dus à l’ensemble des processus impliqués, dont les régulations qui jouent un rôle essentiel dans le phénomène étudié. Ces équations cinétiques prennent en général la forme d’équations différentielles que l’on intègre numériquement [2]. Les solutions obtenues décrivent le comportement du système en fonction des paramètres qui contrôlent son évolution, comme les vitesses maximales de synthèse ou de dégradation de protéines ou d’ARN messagers. De telles simulations numériques permettent de déterminer le comportement du système biologique dans diverses conditions et de prédire sa réponse à une variation de l’un ou l’autre des paramètres de contrôle. La modélisation contribue à mettre en lumière le cœur du mécanisme à l’origine d’un rythme biologique - c’est-à-dire l’ensemble minimal de variables et d’interactions capable de produire le comportement périodique observé - et les conditions précises nécessaires à son déroulement [1, 2].
Des modèles mathématiques ont été proposés pour la plupart des rythmes biologiques, par exemple pour les variations périodiques du potentiel membranaire dans les cellules cardiaques [52] (→) et neuronales, les oscillations du calcium intracellulaire, les réactions enzymatiques oscillantes, et les oscillations de populations de prédateurs et de proies en écologie. Pour illustrer comment se fait l’approche des rythmes en termes de biologie systémique, nous considérerons ici deux rythmes cellulaires aux conséquences physiologiques particulièrement marquantes : l’horloge circadienne et le cycle de division cellulaire. Ces deux exemples montrent comment la compréhension détaillée du mécanisme des rythmes cellulaires peut bénéficier d’une modélisation fondée sur les données de l’expérience. La synergie entre expérience et modélisation a toujours été au cœur de la biologie des systèmes, avant même qu’elle n’adoptât ce nom.
(→) voir l’article de P. Comtois et al., page 57 de ce numéro
La section 2 est consacrée aux rythmes circadiens, prototype de rythme associé à la régulation génétique. Cet exemple illustre non seulement la manière dont la modélisation contribue à clarifier le mécanisme moléculaire d’un rythme, mais aussi les conditions précises dans lesquelles il survient et les troubles physiologiques associés à son dysfonctionnement. L’exemple des rythmes circadiens montre aussi comment la complexité des modèles croît à mesure que de nouvelles données expérimentales s’accumulent. Le cycle cellulaire des cellules de mammifères, examiné dans la section 3, offre un exemple de réseau de régulation complexe dont la structuration en modules permet de mieux appréhender son auto-organisation temporelle sous forme d’oscillations entretenues. La section 4 est consacrée aux perspectives ouvertes par la biologie des systèmes et par son nouvel avatar, la biologie synthétique, dans l’étude des rythmes cellulaires
 .
.
Les rythmes circadiens
D’une période proche de 24 heures, les rythmes circadiens sont observés chez tous les eucaryotes, et chez certains procaryotes comme les cyanobactéries. Ces rythmes permettent aux organismes de s’adapter au caractère périodique de l’environnement terrestre et d’anticiper l’alternance jour/nuit [3]. Les rythmes circadiens peuvent survenir en conditions d’obscurité ou de lumière constante : ils résultent de mécanismes internes à l’organisme et sont donc endogènes. Toutefois, le couplage avec le cycle lumière-obscurité permet la synchronisation de l’horloge circadienne avec la périodicité externe de 24 heures. De nombreuses études expérimentales menées au cours des deux dernières décennies ont permis de clarifier de manière détaillée le mécanisme moléculaire des rythmes circadiens [4–6].
Rythme circadien chez la drosophile
Les premiers travaux sur la génétique des rythmes circadiens ont porté sur le cycle d’activité locomotrice chez la drosophile. Ces travaux montraient que ce comportement est accompagné par des oscillations circadiennes dans la concentration de la protéine PER et de son ARN messager [6, 47]. Le mécanisme du rythme circadien repose sur l’autorégulation négative exercée par la protéine PER sur l’expression de son propre gène [6] et fait intervenir la phosphorylation de la protéine PER, qui conduit à sa dégradation et à son entrée dans le noyau. Un modèle mathématique fondé sur cette régulation (Figure 1A) rend compte des oscillations entretenues de la protéine PER en obscurité constante [7]. L’évolution temporelle des variables du modèle est décrite par un système d’équations différentielles ordinaires couplées. Les cinq variables considérées dans ce modèle représentent les concentrations d’ARN messager et des différentes formes, phosphorylées ou non phosphorylées, cytosoliques ou nucléaires, de la protéine PER. Des études ultérieures ont montré qu’un second gène, nommé tim, joue un rôle essentiel dans le contrôle du rythme circadien par la lumière chez la drosophile. La boucle de régulation négative fait intervenir le complexe PER-TIM qui inhibe l’expression des gènes per et tim. La dégradation de la protéine TIM s’accélère en phase de lumière, ce qui a pour effet de synchroniser les oscillations circadiennes sur le rythme jour/nuit [8]. Le modèle à dix variables fondé sur cette régulation (Figure 1B) prédit à nouveau l’existence d’oscillations entretenues et rend compte de l’entraînement du rythme circadien par le cycle lumière-obscurité [9].
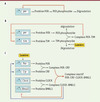 |
Figure 1. Trois modèles de complexité croissante pour les rythmes circadiens. A. Le premier modèle proposé pour les rythmes circadiens chez la drosophile tient compte de la régulation du seul gène per [7]. Le mécanisme de régulation dans ce modèle est fondé sur une boucle de rétroaction négative, la transcription du gène per étant inhibée par son produit, la protéine PER. B. Modèle pour les rythmes circadiens chez la drosophile incorporant le gène tim. Ce modèle tient compte de la formation d’un complexe PER-TIM, d’une boucle de rétroaction négative exercée par ce complexe sur la trancription des gènes per et tim, et de l’effet de la lumière sur la dégradation de la protéine TIM [9]. C. Modèle pour les rythmes circadiens chez les mammifères incorporant les gènes Per, Cry, Clock, Bmal1 ainsi qu’une régulation positive du complexe CLOCK-BMAL1 sur les gènes Per et Cry, une régulation négative de PER-CRY sur l’activité du complexe CLOCK-BMAL1 via la formation d’un complexe tétramérique inactif, une régulation négative de CLOCK-BMAL1, via REV-ERBα (non représenté), sur la transcription de ses propres gènes, et l’induction du gène Per par la lumière [12]. |
L’horloge circadienne chez les mammifères
L’autorégulation négative exercée par les produits des gènes per et tim chez la drosophile est en fait de nature indirecte [10]. On rencontre un jeu similaire de régulations positives et négatives entrecroisées dans le mécanisme de l’horloge circadienne chez les mammifères [11]. La protéine CRY (cryptochrome) forme ici un complexe avec PER. Deux autres protéines, CLOCK et BMAL1 (brain and muscle arnt-like protein-1) en forment un autre qui réprime l’expression du gène Bmal1 et induit celle des gènes Per et Cry. Le complexe PER-CRY se lie avec CLOCK-BMAL1 pour former un complexe inactif (Figure 1C) [46]. La lumière induit l’expression du gène Per et permet de synchroniser l’horloge circadienne sur le cycle lumière-obscurité. L’étude d’un modèle fondé sur ce mécanisme d’autorégulation négative indirecte conduit à plusieurs prédictions [12]. Il révèle par exemple la possibilité de multiples sources d’oscillation dans le réseau de régulation génétique contrôlant les rythmes circadiens. Même en l’absence de protéine PER des oscillations pourraient ainsi se produire en raison de l’autorégulation négative exercée par la protéine BMAL1 par l’entremise de la protéine REV-ERBα [48] sur l’expression de son gène. La complexification progressive des modèles permet aussi d’expliquer ou de prédire l’effet de mutations dans les gènes codant pour de nouveaux facteurs impliqués dans le fonctionnement de l’horloge.
Dysfonctionnements de l’horloge circadienne chez l’homme
Le modèle des rythmes circadiens chez les mammifères nous donne la possibilité d’analyser les bases moléculaires et dynamiques de certains troubles physiologiques liés au dysfonctionnement de l’horloge circadienne chez l’homme. Ces troubles altèrent principalement le cycle veille-sommeil [13] qui est contrôlé à la fois par un mécanisme homéostatique et par l’horloge circadienne. Un cas particulièrement intéressant est celui du syndrome familial d’avance de phase du sommeil (désigné par l’acronyme FASPS en anglais) [14]. Les personnes présentant ce syndrome tombent de sommeil vers 19 h 30 et se réveillent vers 4 h 30 du matin. La durée de la phase de sommeil est donc normale, mais son déclenchement est avancé de plusieurs heures. Ce syndrome est lié à une mutation qui entraîne une phosphorylation moindre de la protéine PER et la réduction de la période autonome de ses oscillations [14]. Un dysfonctionnement de l’horloge circadienne, dû à une mutation, se traduit ainsi par une perturbation du cycle veille-sommeil. La modélisation confirme que la diminution de la période des oscillations autonomes en obscurité constante peut aller de pair avec une avance de phase lors de l’entraînement par le cycle lumière-obscurité [12] (Figure 2). Le syndrome de retard de phase, connu cliniquement, est également observé dans le modèle (Figure 2).
 |
Figure 2. Dysfonctionnements des rythmes circadiens. Oscillations obtenues dans le modèle décrit pour les rythmes circadiens des mammifères (Figure 1C) après entraînement par des cycles jour-nuit (A) et en conditions d’obscurité constante (B) pour des sujets ayant un rythme de sommeil normal ou souffrant de syndromes d’avance (FASPS) ou de retard (DSPS) de phase du sommeil. Dans le cas normal (traits noirs), la période autonome est proche de 24 h (τ = 24,4 h). Pour le FASPS (traits rouges), le maximum des oscillations de transcription du gène Per est avancé de quelques heures lors d’un entraînement et la période autonome est raccourcie d’une heure (τ = 23,4 h). Pour le DSPS (traits bleus), le maximum est retardé lors d’un entraînement et la période est allongée d’environ 2 h (τ = 26,5 h). Les rectangles blancs et gris correspondent respectivement aux phases de lumière et d’obscurité. Les courbes ont été obtenues par intégration numérique des équations du modèle pour les rythmes circadiens chez les mammifères [12] avec les valeurs de paramètres reprises dans le Tableau I de cet article. La vitesse maximum de phosphorylation de la protéine PER, mesurée par le paramètre Vphos, vaut 0,6 nM/h pour le FASPS, 0,85 nM/h pour le cas normal et 1,1 nM/h pour le DSPS. |
Les simulations numériques suggèrent que, dans d’autres conditions, l’horloge circadienne ne peut être entraînée par le cycle lumière-obscurité [12, 15]. De tels troubles du sommeil sont connus en physiologie humaine : chez certains patients, en effet, le rythme veille-sommeil fonctionne en libre cours. La phase du cycle de sommeil est alors décalée chaque jour, tout comme on l’observe dans les cas de cécité. Ce syndrome est connu sous le nom de « non-24 hour sleep-wake cycle syndrome » [13]. Selon leur nature et leur degré, une perturbation ou un dysfonctionnement de l’horloge circadienne ont des implications physiologiques : effet de décalages horaires ou du travail posté, troubles de l’humeur, ou risques accrus de cancérogenèse [16, 17]. L’effet des rythmes biologiques sur l’action des médicaments est l’objet des recherches en chronopharmacologie [18].
Oscillateur mitotique et cycle cellulaire
Le cycle cellulaire joue un rôle essentiel dans la dynamique du vivant. Chez les organismes pluricellulaires, il conditionne le développement et la différenciation ; sa dérégulation sous-tend la prolifération tumorale [19]. Comprendre la dynamique du cycle cellulaire est un défi pour la biologie systémique. Les études expérimentales ont porté tout d’abord sur la forme plus simple que prend le cycle cellulaire aux premiers stades de développement des embryons de grenouille [20]. Par la suite, elles ont analysé le cycle cellulaire chez la levure, et celui des cellules somatiques, en particulier chez les mammifères. De même, la modélisation a tout d’abord porté sur le cycle cellulaire des embryons de grenouille [21, 22], avant de s’adresser à celui de la levure [23] puis des cellules de mammifères [24–26].
Un oscillateur mitotique dans les cellules embryonnaires de grenouille
Le cycle des cellules embryonnaires de grenouille est contrôlé par le facteur MPF (mitosis promoting factor) qui induit la mitose quand son activité atteint un maximum. Le cycle peut être vu comme une oscillation de l’activité du MPF, ce qui justifie le nom d’oscillateur mitotique donné à ce système. Les études expérimentales ont montré que le MPF est un complexe entre une cycline et la protéine kinase cdc2, à présent nommée Cdk1 (le sigle Cdk désigne les kinases dépendantes de cyclines). La kinase cdc2 est inhibée lorsqu’elle est phosphorylée par la kinase wee1, et activée par déphosphorylation sous l’action de la phosphatase cdc25. La synthèse de cycline suffit à faire tourner l’oscillateur mitotique [20]. Le mécanisme des oscillations repose sur un circuit d’autorégulation négative : la synthèse de cycline suscite l’activation de la kinase cdc2, et celle-ci induit la dégradation de la cycline. Un modèle fondé sur cette régulation confirme qu’elle est capable de donner lieu à des oscillations entretenues de la kinase cdc2 [22]. Toutefois, la régulation négative s’accompagne d’une auto-amplification due à l’inhibition de la kinase wee1 par cdc2 d’une part, et à l’activation de la phosphatase cdc25 par cdc2 d’autre part. L’incorporation dans les modèles de telles rétroactions positives montre que l’auto-amplification donne lieu à un phénomène de coexistence entre deux états stationnaires stables. En présence de la rétroaction négative due à l’induction par la cdc2 de la dégradation de la cycline, une telle bistabilité conduit à des oscillations entretenues sous la forme d’un cycle d’hystérèse décrit de manière répétitive. Ces prédictions théoriques ont été vérifiées expérimentalement sur des œufs de grenouille [27, 28].
Complexité du cycle cellulaire de la levure et des cellules de mammifères
Le cycle cellulaire s’avère plus complexe chez la levure et dans les cellules somatiques de mammifères. Le cycle est alors divisé en phases M (mitose), G1, S (réplication de l’ADN), et G2 qui précède une nouvelle phase M. Le passage d’une phase à l’autre est conditionné par des mécanismes de contrôle assurant que la phase qui précède s’est terminée de manière adéquate. Les transitions entre les phases du cycle sont contrôlées par différents couples de kinases Cdk et de cyclines [19]. Ainsi, dans les cellules de mammifères, pour lesquelles la durée du cycle peut atteindre 24 heures ou plus - alors qu’elle n’est que de 30 minutes dans les cellules embryonnaires de grenouille -, le complexe cycline D/Cdk4-6 contrôle la progression dans la phase G1, tandis que la transition G1/S est sous le contrôle du complexe cycline E/Cdk2. Le complexe cycline A/Cdk2 contrôle la transition S/G2, avant que le complexe cycline B/Cdk1 prenne le relais et conduise à la mitose.
La nature répétitive du cycle cellulaire pose la question de savoir si celui-ci peut être considéré comme un rythme cellulaire, à l’image de l’oscillateur mitotique responsable des cycles rapides observés dans les embryons de grenouille. Alors que le modèle pour ce dernier oscillateur comprend un nombre réduit de variables [21, 22], la modélisation du cycle cellulaire des cellules de mammifères s’avère beaucoup plus complexe. Des modèles partiels ont été proposés pour la transition G1/S [24–26, 49].
Un modèle global pour le cycle cellulaire des cellules de mammifères, comprenant quatre modules centrés sur les différents couples de cycline/Cdk contrôlant les phases du cycle, est schématisé dans la Figure 3 [29]. Ce modèle comprend près d’une quarantaine de variables couplées par l’action des Cdk sur les voies de dégradation des cyclines et par de multiples autres régulations. De manière remarquable, le modèle montre que ce système complexe admet un comportement périodique similaire à celui observé dans le modèle beaucoup plus simple proposé pour l’oscillateur mitotique des cellules embryonnaires. Ici, l’activité de chaque couple de cycline/Cdk « s’allume » de manière transitoire avant de retomber quand le complexe suivant s’active (Figure 4). L’activation séquentielle des différents complexes cycline/Cdk correspond à l’enchaînement autonome des diverses phases du cycle cellulaire. Cet enchaînement possède un caractère répétitif, dans la mesure où le réseau de Cdk se comporte comme un oscillateur autonome. Les oscillations se produisent seulement en présence d’un niveau suffisant de facteurs de croissance. Un intérêt du modèle est d’éclairer la nature du point de restriction en phase G1, au-delà duquel la cellule n’a plus besoin de facteur de croissance pour achever son cycle de division [19].
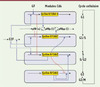 |
Figure 3. Schéma du modèle pour le cycle cellulaire des cellules de mammifères [29]. Le modèle est structuré en quatre modules correspondant aux quatre couples de cycline/Cdk contrôlant les phases successives du cycle cellulaire, G1, S, G2 et M. Les quatre modules sont couplés par le contrôle de la synthèse et de la dégradation des cyclines, la phosphorylation-déphosphorylation des kinases dépendantes de cyclines (Cdk), et le couple d’effecteurs antagonistes E2F et pRB (protéine du rétinoblastome) qui favorisent et freinent, respectivement, la progression dans le cycle cellulaire. Le modèle est décrit par un système de 39 équations différentielles qui se comporte spontanément de manière oscillante (Figure 4) quand le niveau de facteurs de croissance (GF) dépasse une valeur critique. |
 |
Figure 4. Influence du niveau des facteurs de croissance sur les oscillations du cycle cellulaire. Comportement périodique prédit par le modèle pour le cycle cellulaire des cellules de mammifères (voir schéma dans la Figure 3) lorsque le niveau de facteurs de croissance (GF) dépasse un seuil. Les courbes montrent qu’en raison de multiples régulations couplant les variables au sein du système, le réseau de cyclines/Cdk s’auto-organise dans le temps. Cette auto-organisation prend la forme d’oscillations entretenues correspondant à l’activation séquentielle et répétitive des différents couples de cyclines/Cdk contrôlant les phases successives du cycle cellulaire [29]. |
Cycle cellulaire et rythmes circadiens sont liés : l’horloge circadienne, par l’intermédiaire de la protéine BMAL1, induit l’expression du gène codant pour la protéine kinase Wee1 qui inhibe la kinase Cdk1 et, par là, la transition G2/M [30]. En raison de ce couplage et d’autres du même type, le cycle cellulaire peut être entraîné par l’horloge circadienne de telle sorte que la fraction de cellules en phase S varie avec une périodicité de 24 h. Les conséquences d’un tel couplage pour la chronopharmacologie anticancéreuse ont été étudiées de manière clinique et théorique [31].
Discussion et perspectives
Les exemples des rythmes circadiens et du cycle cellulaire montrent comment l’organisation temporelle peut naître spontanément au sein des réseaux de régulation enzymatique ou génétique. Cette auto-organisation sous forme d’oscillations entretenues représente clairement une propriété systémique associée aux boucles de rétroaction qui relient les différents nœuds du réseau de régulation. La biologie des systèmes offre un cadre naturel pour l’étude de ces comportements dynamiques, dont l’approche bénéficie d’une synergie entre expérience et modélisation.
Nouveaux rythmes, nouveaux oscillateurs
Au cours des années récentes, de nouveaux rythmes sont venus enrichir le répertoire déjà fourni des comportements oscillants au niveau cellulaire. Ainsi, des oscillations d’une période de quelques heures ont été observées dans la synthèse du facteur de transcription NF-κB [32] et du répresseur de tumeur p53 [33]. Des expériences récentes [34] montrent que les oscillations de NF-κB peuvent être entraînées par une stimulation périodique par des signaux comme le TNFα (tumor necrosis factor) dont la fréquence module l’expression des gènes contrôlés par NF-κB. D’autre part, le transport oscillant du facteur de transcription Msn2 entre cytoplasme et noyau a été observé chez la levure en réponse au stress ; le phénomène d’une période de quelques minutes paraît lié à des oscillations d’AMP cyclique [35]. Des oscillations similaires ont été observées pour le facteur de transcription Crz1 [36].
L’un des exemples les plus remarquables de rythme cellulaire, découvert il y a une dizaine d’années, est celui de l’horloge de segmentation qui contrôle la formation périodique des somites au cours de l’embryogenèse chez les vertébrés. La périodicité spatiale représente une trace permanente de la périodicité temporelle qui lui a donné naissance [37]. Le mécanisme de l’horloge de segmentation n’a pas encore été élucidé, mais cette horloge implique des oscillations coordonnées dans l’expression de gènes appartenant aux trois voies de signalisation Notch, FGF (fibroblast growth factor), et Wnt [38]. La modélisation de l’horloge de segmentation a été entreprise en plusieurs étapes. Les premiers modèles rendant compte des oscillations de la voie Notch sont fondés sur l’autorégulation négative de l’expression du gène Hes (hairy enhancer of split) chez le poisson zèbre [39]. Un modèle fondé sur le couplage des voies Wnt et Notch fut ensuite proposé [40]. Enfin, un modèle récent considère le couplage entre les trois voies de signalisation qui chacune fonctionne de manière oscillante en raison de l’existence de rétroactions négatives [41].
L’avènement de la biologie synthétique
L’étude des réseaux oscillants connaît une transition avec l’avènement de la biologie synthétique. Plusieurs réseaux de régulation génétique ont été conçus de manière théorique avant d’être synthétisés par expression chez E. coli [50]. Le premier réseau de ce type, connu sous le nom de Répressilateur, formé par trois répresseurs organisés de manière cyclique, a été construit voici près de dix ans [42]. Depuis, d’autres réseaux génétiques oscillants ont été synthétisés [43–45]. À côté des travaux consacrés aux nombreux rythmes qui scandent la dynamique cellulaire, la biologie synthétique ouvre ainsi des voies prometteuses à la compréhension des rythmes du vivant.
De manière plus générale, les modèles représentent un complément essentiel à l’étude expérimentale des systèmes biologiques. Ils permettent de les étudier dans des situations diverses, de tester des hypothèses, de déterminer les conséquences d’une modification d’un mécanisme de régulation - par exemple, l’introduction d’une nouvelle rétroaction de nature positive ou négative -, et de prédire l’effet d’une variation des paramètres sur le comportement dynamique du système, ce qui met en lumière les paramètres clés dont l’influence s’avère la plus marquante. Les modèles éclairent l’origine des dysfonctionnements physiologiques, comme on peut le voir pour les rythmes circadiens et la prolifération tumorale. En pharmacologie, la modélisation aide à préciser les schémas optimaux d’administration de médicaments - une telle approche s’applique à la chronothérapie du cancer en combinant la modélisation de l’administration circadienne de médicaments anticancéreux avec celle du cycle cellulaire [31]. Consubstantielle à la biologie des systèmes, la modélisation contribue à mieux cibler les expérimentations biologiques, pharmacologiques, thérapeutiques ou cliniques et à saisir en profondeur les mécanismes qui sous-tendent la dynamique du vivant.
Conflit d’intérêts
Les auteurs déclarent n’avoir aucun conflit d’intérêts concernant les données publiées dans cet article
Remerciements
Nos travaux sont soutenus par le Fonds de la recherche scientifique médicale (FRSM, convention #3.4636.04), l’Union européenne à travers le Réseau d’excellence BioSim (contrat n° LSHB-CT-2004-005137), et le Programme des Pôles d’attraction interuniversitaires (projet P6/25, BioMaGNet) géré par les services fédéraux de la politique scientifique. JCL est chercheur qualifié du FNRS, et CG bénéficie d’une bourse du FRIA (Belgique).
Références
- Goldbeter A. Biochemical oscillations and cellular rhythms : the molecular bases of periodic and chaotic behavior. Cambridge, UK : Cambridge University Press, 1996 : 606 p. [Google Scholar]
- Goldbeter A. Computational approaches to cellular rhythms. Nature 2002; 420 : 238–45. [Google Scholar]
- Moore-Ede MC, Sulzman FM, Fuller CA. The clocks that time us. Physiology of the circadian timing system. Cambridge, MA : Harvard University Press, 1982 : 448 p. [Google Scholar]
- Young MW, Kay SA. Time zones: a comparative genetics of circadian clocks. Nat Rev Genet 2001; 2 : 702–15. [Google Scholar]
- Reppert SM, Weaver DR. Coordination of circadian timing in mammals. Nature 2002; 418 : 935–41. [Google Scholar]
- Hardin PE, Hall JC, Rosbash M. Feedback of the Drosophila period gene product on circadian cycling of its messenger RNA levels. Nature 1990; 343 : 536–40. [Google Scholar]
- Goldbeter A. A model for circadian oscillations in the Drosophila period protein (PER). Proc R Soc Lond B 1995; 261 : 319–24. [Google Scholar]
- Zeng H, Qian Z, Myers MP, et al. A light-entrainment mechanism for the Drosophila circadian clock. Nature 1996; 380 : 129–35. [Google Scholar]
- Leloup JC, Goldbeter A. A model for circadian rhythms in Drosophila incorporating the formation of a complex between the PER and TIM proteins. J Biol Rhythms 1998; 13 : 70–87. [Google Scholar]
- Glossop NRJ, Lyons LC, Hardin PE. Interlocked feedback loops within the Drosophila circadian oscillator. Science 1999; 286 : 766–8. [Google Scholar]
- Shearman LP, Sriram S, Weaver DR, et al. Interacting molecular loops in the mammalian circadian clock. Science 2000; 288 : 1013–9. [Google Scholar]
- Leloup JC, Goldbeter A. Toward a detailed computational model for the mammalian circadian clock. Proc Natl Acad Sci USA 2003; 100 : 7051–6. [Google Scholar]
- Richardson GS, Malin HV. Circadian rhythm sleep disorders: Pathophysiology and treatment. J Clin Neurophysiol 1996; 13 : 17–31. [Google Scholar]
- Toh KL, Jones CR, He Y, et al. An hPer2 phosphorylation site mutation in familial advanced sleep phase syndrome. Science 2001; 291 : 1040–3. [Google Scholar]
- Leloup JC, Goldbeter A. Modeling the circadian clock: from molecular mechanism to physiological disorders. BioEssays 2008; 30 : 590–600. [Google Scholar]
- Fu L, Pelicano H, Liu J, et al. The circadian gene period2 plays an important role in tumor suppression and DNA damage response in vivo. Cell 2002; 111 : 41–50. [Google Scholar]
- Filipski E, King VM, Li X, et al. Host circadian clock as a control point in tumor progression. J Natl Cancer Inst 2002; 94 : 690–7. [Google Scholar]
- Lévi F, Schibler U. Circadian rhythms: mechanisms and therapeutic implications. Annu Rev Pharmacol Toxicol 2007; 47 : 593–628. [Google Scholar]
- Morgan DO. The cell cycle: principles of control. Oxford, UK : Oxford University Press, 2006 : 298 p. [Google Scholar]
- Murray AW, Kirschner MW. Cyclin synthesis drives the early embryonic cell cycle. Nature 1989; 339 : 275–80. [Google Scholar]
- Tyson JJ. Modeling the cell division cycle: cdc2 and cyclin interactions. Proc Natl Acad Sci USA 1991; 88 : 7328–32. [Google Scholar]
- Goldbeter A. A minimal cascade model for the mitotic oscillator involving cyclin and cdc2 kinase. Proc Natl Acad Sci USA 1991; 88 : 9107–11. [Google Scholar]
- Chen KC, Calzone L, Csikasz-Nagy A, et al. Integrative analysis of cell cycle control in budding yeast. Mol Biol Cell 2004; 15 : 3841–62. [Google Scholar]
- Qu Z, Weiss JN, MacLellan WR. Regulation of the mammalian cell cycle: a model of the G1-to-S transition. Am J Physiol Cell Physiol 2003; 284 : 349–64. [Google Scholar]
- Swat M, Kel A, Herzel H. Bifurcation analysis of the regulatory modules of the mammalian G1/S transition. Bioinformatics 2004; 20 : 1506–11. [Google Scholar]
- Novak B, Tyson JJ. A model for restriction point control of the mammalian cell cycle. J Theor Biol 2004; 230 : 563–79. [Google Scholar]
- Sha W, Moore J, Chen K, et al. Hysteresis drives cell-cycle transitions in Xenopus laevis egg extracts. Proc Natl Acad Sci USA 2003; 100 : 975–80. [Google Scholar]
- Pomerening JR, Sontag ED, Ferrel Jr JE. Building a cell cycle oscillator : hysteresis and bistability in the activation of Cdc2. Nat Cell Biol 2003; 5 : 346–51. [Google Scholar]
- Gérard C, Goldbeter A. Temporal self-organization of the cyclin/Cdk network driving the mammalian cell cycle. Proc Natl Acad Sci USA 2009; 106 : 21643–8. [Google Scholar]
- Matsuo T, Yamaguchi S, Mitsui S, et al. Control mechanism of the circadian clock for timing of cell division in vivo. Science 2003; 302 : 255–9. [Google Scholar]
- Altinok A, Lévi F, Goldbeter A. A cell cycle automaton model for probing circadian patterns of anticancer drug delivery. Adv Drug Deliv Rev 2007; 59 : 1036–53. [Google Scholar]
- Nelson DE, Ihekwaba AE, Elliott M, et al. Oscillations in NF-kappaB signaling control the dynamics of gene expression. Science 2004; 306 : 704–8. [Google Scholar]
- Lev Bar-Or R, Maya R, Segel LA, et al. Generation of oscillations by the p53-Mdm2 feedback loop: a theoretical and experimental study. Proc Natl Acad Sci USA 2000; 97 : 11250–5. [Google Scholar]
- Ashall L, Horton CA, Nelson DE, et al. Pulsatile stimulation determines timing and specificity of NF-kappaB-dependent transcription. Science 2009; 324 : 242–6. [Google Scholar]
- Garmendia-Torres C, Goldbeter A, Jacquet M. Nucleocytoplasmic oscillations of the yeast transcription factor Msn2: evidence for periodic PKA activation. Curr Biol 2007; 17 : 1044–9. [Google Scholar]
- Cai L, Dalal CK, Elowitz MB. Frequency-modulated nuclear localization bursts coordinate gene regulation. Nature 2008; 455 : 485–90. [Google Scholar]
- Pourquié O. The segmentation clock: converting embryonic time into spatial pattern. Science 2003; 301 : 328–30. [Google Scholar]
- Dequeant ML, Glynn E, Gaudenz K, et al. A complex oscillating network of signaling genes underlies the mouse segmentation clock. Science 2006; 314 : 1595–8. [Google Scholar]
- Lewis J. Autoinhibition with transcriptional delay: a simple mechanism for the zebrafish somitogenesis oscillator. Curr Biol 2003; 13 : 1398–408. [Google Scholar]
- Rodriguez-Gonzalez JG, Santillan M, Fowler AC, et al. The segmentation clock in mice: Interaction between the Wnt and Notch signalling pathways. J Theor Biol 2007; 248 : 37–47. [Google Scholar]
- Goldbeter A, Pourquié O. Modeling the segmentation clock as a network of coupled oscillations in the Notch, Wnt and FGF signaling pathways. J Theor Biol 2008; 252 : 574–85. [Google Scholar]
- Elowitz MB, Leibler S. A synthetic oscillatory network of transcriptional regulators. Nature 2000; 403 : 335–8. [Google Scholar]
- Atkinson MR, Savageau MA, Myers JT, et al. Development of genetic circuitry exhibiting toggle switch or oscillatory behavior in Escherichia coli. Cell 2003; 113 : 597–607. [Google Scholar]
- Stricker J, Cookson S, Bennett MR, et al. A fast, robust and tunable synthetic gene oscillator. Nature 2008; 456 : 516–9. [Google Scholar]
- Tigges M, Marquez-Lago TT, Stelling J, et al. A tunable synthetic mammalian oscillator. Nature 2009; 457 : 309–12. [Google Scholar]
- Dardente H. Redondance génétique et synchronisation cellulaire dans les horloges circadiennes. Med Sci (Paris) 2008; 24 : 270–6. [Google Scholar]
- Rouyer F. Des horloges du matin et du soir dans le cerveau de la drosophile. Med Sci (Paris) 2005; 21 : 808–10. [Google Scholar]
- Teboul M, Delaunay F. Le récepteur nucléaire orphelin Rev-erbalpha oscille entre répression et activation. Med Sci (Paris) 2003; 19 : 411–3. [Google Scholar]
- Pommier Y, Kohn KW. Cycle cellulaire et points de contrôle en oncologie : nouvelles cibles thérapeutiques. Med Sci (Paris) 2003; 19 : 173–86. [Google Scholar]
- Danchin A. Saurons-nous construire une bactérie synthétique ? Med Sci (Paris) 2008; 24 : 533–40. [Google Scholar]
- Lesne A. Biologie des systèmes : l’organisation multiéchelle des systèmes vivants. Med Sci (Paris) 2009; 25 : 585–7. [Google Scholar]
- Comtois P, Potse M, Vinet A. Approche multi-échelle appliquée à la modélisation de l’activité électrique du cœur. Med Sci (Paris) 2010; 26 : 57–63. [Google Scholar]
Liste des tableaux
Liste des figures
 |
Figure 1. Trois modèles de complexité croissante pour les rythmes circadiens. A. Le premier modèle proposé pour les rythmes circadiens chez la drosophile tient compte de la régulation du seul gène per [7]. Le mécanisme de régulation dans ce modèle est fondé sur une boucle de rétroaction négative, la transcription du gène per étant inhibée par son produit, la protéine PER. B. Modèle pour les rythmes circadiens chez la drosophile incorporant le gène tim. Ce modèle tient compte de la formation d’un complexe PER-TIM, d’une boucle de rétroaction négative exercée par ce complexe sur la trancription des gènes per et tim, et de l’effet de la lumière sur la dégradation de la protéine TIM [9]. C. Modèle pour les rythmes circadiens chez les mammifères incorporant les gènes Per, Cry, Clock, Bmal1 ainsi qu’une régulation positive du complexe CLOCK-BMAL1 sur les gènes Per et Cry, une régulation négative de PER-CRY sur l’activité du complexe CLOCK-BMAL1 via la formation d’un complexe tétramérique inactif, une régulation négative de CLOCK-BMAL1, via REV-ERBα (non représenté), sur la transcription de ses propres gènes, et l’induction du gène Per par la lumière [12]. |
| Dans le texte | |
 |
Figure 2. Dysfonctionnements des rythmes circadiens. Oscillations obtenues dans le modèle décrit pour les rythmes circadiens des mammifères (Figure 1C) après entraînement par des cycles jour-nuit (A) et en conditions d’obscurité constante (B) pour des sujets ayant un rythme de sommeil normal ou souffrant de syndromes d’avance (FASPS) ou de retard (DSPS) de phase du sommeil. Dans le cas normal (traits noirs), la période autonome est proche de 24 h (τ = 24,4 h). Pour le FASPS (traits rouges), le maximum des oscillations de transcription du gène Per est avancé de quelques heures lors d’un entraînement et la période autonome est raccourcie d’une heure (τ = 23,4 h). Pour le DSPS (traits bleus), le maximum est retardé lors d’un entraînement et la période est allongée d’environ 2 h (τ = 26,5 h). Les rectangles blancs et gris correspondent respectivement aux phases de lumière et d’obscurité. Les courbes ont été obtenues par intégration numérique des équations du modèle pour les rythmes circadiens chez les mammifères [12] avec les valeurs de paramètres reprises dans le Tableau I de cet article. La vitesse maximum de phosphorylation de la protéine PER, mesurée par le paramètre Vphos, vaut 0,6 nM/h pour le FASPS, 0,85 nM/h pour le cas normal et 1,1 nM/h pour le DSPS. |
| Dans le texte | |
 |
Figure 3. Schéma du modèle pour le cycle cellulaire des cellules de mammifères [29]. Le modèle est structuré en quatre modules correspondant aux quatre couples de cycline/Cdk contrôlant les phases successives du cycle cellulaire, G1, S, G2 et M. Les quatre modules sont couplés par le contrôle de la synthèse et de la dégradation des cyclines, la phosphorylation-déphosphorylation des kinases dépendantes de cyclines (Cdk), et le couple d’effecteurs antagonistes E2F et pRB (protéine du rétinoblastome) qui favorisent et freinent, respectivement, la progression dans le cycle cellulaire. Le modèle est décrit par un système de 39 équations différentielles qui se comporte spontanément de manière oscillante (Figure 4) quand le niveau de facteurs de croissance (GF) dépasse une valeur critique. |
| Dans le texte | |
 |
Figure 4. Influence du niveau des facteurs de croissance sur les oscillations du cycle cellulaire. Comportement périodique prédit par le modèle pour le cycle cellulaire des cellules de mammifères (voir schéma dans la Figure 3) lorsque le niveau de facteurs de croissance (GF) dépasse un seuil. Les courbes montrent qu’en raison de multiples régulations couplant les variables au sein du système, le réseau de cyclines/Cdk s’auto-organise dans le temps. Cette auto-organisation prend la forme d’oscillations entretenues correspondant à l’activation séquentielle et répétitive des différents couples de cyclines/Cdk contrôlant les phases successives du cycle cellulaire [29]. |
| Dans le texte | |
Les statistiques affichées correspondent au cumul d'une part des vues des résumés de l'article et d'autre part des vues et téléchargements de l'article plein-texte (PDF, Full-HTML, ePub... selon les formats disponibles) sur la platefome Vision4Press.
Les statistiques sont disponibles avec un délai de 48 à 96 heures et sont mises à jour quotidiennement en semaine.
Le chargement des statistiques peut être long.




