| Issue |
Med Sci (Paris)
Volume 30, Novembre 2014
2e colloque de l’ITMO Santé publique – Médecine « personnalisée » et innovations biomédicales : enjeux de santé publique, économiques, éthiques et sociaux (Paris, 5 décembre 2013)
|
|
|---|---|---|
| Page(s) | 23 - 26 | |
| Section | Session 2. Échanges Nord-Sud et innovations biomédicales | |
| DOI | https://doi.org/10.1051/medsci/201430s205 | |
| Published online | 17 November 2014 | |
Modèles mathématiques dynamiques pour la médecine personnalisée
Mathematical dynamical models for personalized medicine
Inserm U897, INRIA SISTM ( statistics in systems biology and translational medicine), université de Bordeaux, ISPED (institut de santé publique, d’épidémiologie et de développement), CHU de Bordeaux, unité de soutien méthodologique à la recherche clinique et épidémiologique, Bordeaux, France ;
institut de recherche vaccinale (Labex) UPEC, Créteil, France
*
rodolphe.thiebaut@isped.u-bordeaux2.fr
Une des conditions nécessaires à la mise en œuvre d’une médecine personnalisée est l’obtention de prédictions individuelles de qualité. Outre l’obtention de mesures toujours plus nombreuses (données « -omiques »), la méthode d’analyse de données est également un élément potentiellement majeur. Nous présentons un exemple d’utilisation de modèles mathématiques dynamiques mécanistes utilisables pour l’adaptation des traitements antirétroviraux de patients infectés par le virus de l’immunodéficience humaine. L’intérêt de ce type d’approche est de construire un modèle sur des connaissances biologiques de l’interaction entre les différents marqueurs et permettre ainsi, potentiellement, une puissance prédictive accrue.
Abstract
One of the necessary conditions to perform any personalized medicine is to obtain good individual predictions. In addition to the numerous markers available (omics data), the methods used to analyze the data are very important too. We are presenting an example of mathematical dynamical mechanistic model that could be used for adapting the antiretroviral treatment in patients infected by the human immunodeficiency virus. The interest of this type of approach is to build a model based on biological knowledge about the interaction between markers and therefore to allow for a better predictive power.
Ce texte fait partie du numéro hors série n° 2/2014 de médecine/sciences (m/s hs2 novembre 2014, vol. 30,) relatant les interventions faites lors du 2e colloque de l’ITMO Santé publique - Médecine « personnalisée » et innovations biomédicales : enjeux de santé publique, économiques, éthiques et sociaux (5 décembre 2013).
© 2014 médecine/sciences – Inserm

La médecine personnalisée est un des objectifs actuels de la recherche médicale. Il s’agit de tenir compte des caractéristiques individuelles pour la prise en charge d’un patient. Nous présentons dans cet article un exemple d’apport de la modélisation mathématique dans ce domaine, en particulier dans le cadre de l’infection par le virus de l’immunodéficience humaine (VIH).
Quelques conditions nécessaires pour une médecine personnalisée
La médecine personnalisée nécessite une bonne prédiction du devenir du patient, sachant l’intervention choisie et ses caractéristiques au moment de l’intervention. La qualité de la prédiction dépend au moins de deux éléments : la qualité des données et la qualité du modèle utilisé pour calculer ces prédictions.
Les données sont de plus en plus nombreuses [1] et suscitent d’ailleurs un enthousiasme récent pour la médecine personnalisée. Par exemple, les données génomiques – notamment l’existence ou non d’une mutation BRCA (breast cancer) - sont devenues une source d’information utile pour la prise en charge du cancer du sein. Cependant, comme discuté par de nombreux auteurs, les données génomiques ne permettent pas d’expliquer la totalité de la variabilité de l’incidence ou de la progression des pathologies [2]. La médecine personnalisée ne s’arrête pas à la médecine génomique, et les données biologiques et cliniques recueillies, tout aussi volumineuses, doivent également être prises en compte.
Les méthodes mathématiques et statistiques utilisées pour réaliser des prédictions sont nombreuses avec, notamment, des techniques d’apprentissage [3], des modèles descriptifs tels que les modèles de régression (modèles logistiques, modèles de survie, etc.), et des modèles dynamiques mécanistes. C’est ce dernier type de modèle que nous allons présenter brièvement dans cet article. Ces modèles sont basés sur des systèmes d’équations différentielles issues de la traduction mathématique de modèles biologiques.
Le contexte de l’infection par le VIH
L’infection par le VIH (virus de l’immunodéficience humaine) est un bon exemple pour la médecine personnalisée dans la mesure où les caractéristiques individuelles influencent déjà un certain nombre d’adaptations de la prescription du traitement antirétroviral [4]. Depuis le milieu des années 1990, les patients infectés par le VIH bénéficient de traitements antirétroviraux hautement actifs, combinant de nombreuses molécules différentes, en général dans le cadre de multithérapies. Le choix du traitement est adapté en fonction de multiples critères [4].
Deux exemples reconnus de médecine personnalisée dans le domaine du VIH utilisent des informations génétiques. Le premier exemple se base sur une propriété du virus : le tropisme CCR5 (C-C chemokine receptor type 5). En effet, le VIH pénètre les cellules en utilisant le récepteur CD4 et un corécepteur qui peut être CXCR4 (C-X-C chemokine receptor type 4) ou CCR5. Or, depuis quelques années, un antirétroviral appelé le maraviroc est disponible ; il permet d’inhiber l’entrée du virus via le CCR5. Pour que le maraviroc soit efficace, il faut bien entendu que la majorité des virus circulant chez un patient aient un tropisme CCR5, c’est-à-dire utilisent ce corécepteur. Pour s’en assurer, le tropisme du virus est mesuré via des tests fonctionnels ou de séquençage [5] avant la prescription de cette molécule. Un autre exemple concerne une caractéristique génétique du patient : son groupe HLA (human leucocyte antigens). Les patients HLA-B*5701 ont un risque majoré d’hypersensibilité à un inhibiteur nucléosidique de la transcriptase inverse appelé abacavir. La recherche de l’allèle HLA-B*5701 est donc préalable à toute prescription d’abacavir. Une autre part de la médecine personnalisée est la surveillance de la réponse au traitement et l’adaptation de ce traitement en fonction de la réponse. Des questions actuelles s’inscrivent dans cette problématique : comment éviter certaines classes thérapeutiques, comme les inhibiteurs de protéase par exemple ? Comment alléger le traitement en limitant les prises hebdomadaires [6] ? Les modèles dynamiques mécanistes sont particulièrement adaptés à ce type de questionnement.
Les modèles mathématiques dynamiques mécanistes
Nous entendons ici par modèles dynamiques mécanistes les modèles basés sur un système d’équations différentielles. Les modèles mécanistes sont très utilisés en pharmacocinétique/pharmacodynamique où ils sont appelés modèles compartimentaux car ils décrivent la diffusion des molécules à travers différents compartiments de l’organisme. Ils sont également utilisés en écologie, où l’on parle de modèles proies-prédateurs, et également pour la modélisation d’épidémies dans une population. Dans le cadre de l’infection par le VIH, ils ont rencontré un grand succès du fait de leur utilisation pour l’estimation de la demi-vie des cellules infectées et du virion ; ils ont permis de démontrer le turnover intense des cellules lymphocytaires et du virus [7]. Brièvement, il s’agit de partir d’un modèle biologique supposé connu et d’utiliser le mécanisme physiopathologique pour spécifier les équations mathématiques. Par exemple, il a été démontré que le VIH infecte essentiellement des cellules lymphocytaires T CD4+. Ces dernières, quand elles sont infectées, produisent du virion. Ce cycle est représenté schématiquement dans la Figure 1.
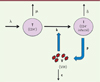 |
Figure 1. Modèle d’infection par le VIH. dT : variation du nombre ou de la concentration de lymphocytes T CD4+ ; dt : intervalle de temps ; λ : taux de production de cellules de novo ; µ : taux de mortalité des cellules ; T : nombre de cellules présentes ; I : nombre de cellules infectées ; V : nombre de virions circulants ; k : taux d’infection (infectivité) ; dV : variation du nombre de virions ; pI : nombre de virions produits ; p : taux de production par cellules ; c : clairance du virus. |
Ce modèle peut alors être traduit sous forme d’équations mathématiques, comme suit :
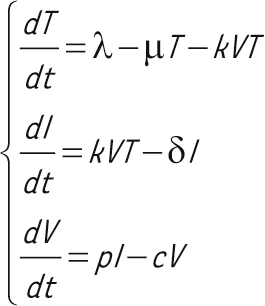
Autrement dit, la variation du nombre ou de la concentration de lymphocytes T CD4+ (dT) pendant un petit intervalle de temps (dt) est fonction d’une constante (taux de production de cellules de novo λ), du taux de mortalité des cellules (µ) proportionnellement au nombre de cellules présentes (T), et du nombre de cellules infectées qui quittent ce « compartiment » pour rejoindre le compartiment des cellules infectées (I). Le nombre de cellules infectées est donc fonction du nombre de cellules cibles, du nombre de virions circulants (V) et du taux d’infection k aussi appelé infectivité. Ce terme quadratique dit d’action de masse est très important pour la compréhension de la dynamique du système et sera repris par la suite. La variation du nombre de virions (dV) par unité de temps dépend du nombre de virions produits (pI), p étant le taux de production par cellule, et de la clairance c du virus.
Le modèle peut ensuite être perfectionné en faisant dépendre certains paramètres d’autres variables. Par exemple, l’infectivité du virus peut dépendre de la dose de traitement antirétroviral, de sa concentration via des fonctions pharmacologiques, ou encore de l’existence de mutations virales, voire même génétiques, de l’hôte. On peut aussi faire dépendre les paramètres d’effets individus-aléatoires ce qui permet, non seulement de prédire des valeurs individuelles (via les estimateurs bayésiens empiriques), mais aussi de quantifier la variabilité inter-individuelle d’un paramètre qui n’est pas expliquée par les variables mesurées (via la variance de l’effet aléatoire portant sur le paramètre considéré).
Le défi est ensuite d’estimer les paramètres de ce modèle avec des données. Il s’agit d’un exercice particulièrement difficile, aussi appelé problème inverse, surtout lorsque tous les composants ne sont pas mesurés et que les données sont déséquilibrées (données manquantes). Cette problématique concerne essentiellement le champ de la statistique. Une approche dite « fréquentiste » basée sur le maximum de vraisemblance, est possible, mais se heurte parfois à un problème de non-identifiabilité : il y a non-identifiabilité si des valeurs différentes des paramètres fournissent le même ajustement aux données. Dans ce cas, une approche bayésienne populationnelle, dans laquelle les paramètres sont estimés en une fois sur l’ensemble des patients de la population, et l’utilisation de connaissances a priori sur les valeurs des paramètres, peuvent être très efficaces [8].
Application dans l’infection par le VIH
Plusieurs applications de ce type d’approche ont été réalisées dans l’infection par le VIH avec, par exemple, l’intégration de données de résistance du virus [9] ou des données de pharmacogénétique [10]. Nous détaillons l’application de ce type d’approche dans l’essai ALBI ANRS 070 qui comparait trois stratégies de traitement antirétroviral basées sur une bithérapie d’analogues nucléosidiques : AZT (azidothymidine)+3TC (lamivudine), ddI (didanosine)+d4T (stavudine) pendant 24 semaines, et un groupe d’alternance traité par AZT+3TC pendant 12 semaines puis par ddI+d4T après 12 semaines. Le résultat publié de cet essai était une supériorité de l’association ddI+d4T en termes de niveau de lymphocytes T CD4+ et de charge virale plasmatique du VIH atteints à 6 mois [11]. En fait, chez les patients des trois groupes, la charge virale diminuait initialement avec la même amplitude. Mais, après cette réponse initiale, on observait un rebond virologique dans le groupe AZT+3TC qui n’était pas expliqué par la survenue plus fréquente de résistances aux antirétroviraux [12]. Le sous-dosage de l’AZT, utilisé à la dose quotidienne de 500 mg au lieu des 600 mg usuels, était discuté [13].
Nous avons proposé un modèle dynamique mécanistique, présenté ailleurs [14], qui incluait l’effet des analogues nucléosidiques sur l’infectivité du virus. En effet, en bloquant la transcription inverse de l’ARN en ADN, ces molécules empêchent l’infection de la cellule. L’estimation faite avec les données des deux groupes, AZT+3TC versus ddI+d4T de l’essai ALBI ANRS 070, a permis d’estimer une différence statistiquement significative (p < 0,0001) d’efficacité entre les deux bithérapies (72 % versus 74 %) sur l’infectivité du virus. L’effet était suffisamment important (> 70 %) pour permettre une chute de la charge virale identique entre les deux groupes. Cependant, cette chute de charge virale était associée à une augmentation du nombre de cellules lymphocytaires T CD4+, qui sont aussi des cibles du virus. Le blocage de l’infectivité était alors insuffisant dans le groupe AZT+3TC au regard de l’augmentation du nombre de cellules cibles, engendrant une augmentation du nombre de cellules infectées et, donc, de virus. Autrement dit, il y avait une reprise de l’épidémie chez l’hôte s’expliquant aussi par un taux de reproduction R0 supérieur à 1, ce qui n’était pas le cas pour le groupe traité par ddI+d4T.
Une fois obtenu un modèle permettant de bien représenter les données des deux groupes traités par AZT+3TC ou ddI+d4T, il est possible de prédire individuellement les trajectoires de réponse au traitement chez les patients du troisième groupe dit d’alternance. Statistiquement, il s’agit d’estimer les valeurs moyennes en population des paramètres avec celles des deux autres groupes. On utilise alors, pour chaque patient, les mesures de charge virale et de CD4 observées lors de la réponse au traitement dans la période initiale sous d4t+ddI pour le groupe alternance, pour inférer la valeur des paramètres individuels. Nous avons alors obtenu des prédictions individuelles pour la réponse lors de la deuxième période sous AZT+3TC tout à fait valides, et donc très proches des valeurs effectivement observées et non utilisées dans le modèle [15].
Le modèle a ensuite été enrichi pour intégrer les modifications de dose de traitement au cours du temps. Nous avons alors montré la qualité des prédictions de la mesure suivante tenant compte du traitement effectivement pris [15]. Ayant validé les qualités prédictives du modèle, des stratégies d’adaptation de traitement peuvent être proposées comme, par exemple, l’optimisation de la dose de traitement [15]. Ces stratégies ne sont encore qu’au stade de preuve de concept, car elles nécessitent un approfondissement de la compréhension et de la modélisation des mécanismes biologiques (comme, dans ce cas, l’apparition accélérée de mutations en cas de sous-dosage), ainsi que le développement d’un outil ergonomique pour le clinicien. Cependant, de telles méthodes constituent à long terme un axe d’évolution des pratiques cliniques.
Conclusion
Ce type d’approche, basée à la fois sur le développement de modèles dynamiques mécanistes et sur la méthode statistique, pourrait être particulièrement utile pour la mise en place d’une médecine personnalisée, notamment pour l’adaptation du traitement en fonction de la réponse initiale. La qualité des prédictions dépend de la pertinence du modèle qui, aujourd’hui, peut être suffisamment complexifié étant donné la croissance récente de la quantité d’information mesurée. C’est la rencontre entre la biologie des systèmes et la pharmacodynamique [16].
Liens d’intérêt
Les auteurs déclarent n’avoir aucun lien d’intérêt concernant les données publiées dans cet article.
Références
- Thiébaut R, Hejblum B, Richert L. L’analyse des Big Data en recherche clinique. Rev Epidemiol Sante Publ 2014 ; 62 : 1–4. [CrossRef] [Google Scholar]
- Chakravarti A. Genomics is not enough. Science 2011 ; 334 : 15. [CrossRef] [PubMed] [Google Scholar]
- Laan MJ van der, Polley EC, Hubbard AE. Super learner. Stat Appl Genet Mol Biol 2007 ; 6 : 25. [Google Scholar]
- Pavlos R, Phillips EJ. Individualization of antiretroviral therapy. Pharmgenomics Pers Med 2012 ; 5 : 1–17. [PubMed] [Google Scholar]
- Raymond S, Delobel P, Izopet J. Phenotyping methods for determining HIV tropism and applications in clinical settings. Curr Opin HIV AIDS 2012 ; 7 : 463–469. [CrossRef] [PubMed] [Google Scholar]
- Ananworanich J, Gayet Ageron A, Braz M. Le, et al. CD4-guided scheduled treatment interruptions compared with continuous therapy for patients infected with HIV-1: results of the Staccato randomised trial. Lancet 2006 ; 368 : 459–465. [CrossRef] [PubMed] [Google Scholar]
- Perelson AS, Neumann AU, Markowitz M, et al. HIV-1 dynamics in vivo: virion clearance rate, infected cell life-span, and viral generation time. Science 1996 ; 271 : 1582–1586. [CrossRef] [PubMed] [Google Scholar]
- Drylewicz J, Commenges D, Thiébaut R, et al. Maximum a posteriori estimation in dynamical models of primary HIV infection. Stat Commun Infect Dis 2012 ; doi : 10.1515/1948-4690.1040. [Google Scholar]
- Vergu E, Mallet A, Golmard JL. Available clinical markers of treatment outcome integrated in mathematical models to guide therapy in HIV infection. J Antimicrob Chemother 2004 ; 53 : 140–143. [CrossRef] [PubMed] [Google Scholar]
- Bertrand J, Treluyer JM, Panhard X, et al. Influence of pharmacogenetics on indinavir disposition and short-term response in HIV patients initiating HAART. Eur J Clin Pharmacol 2009 ; 65 : 667–678. [CrossRef] [PubMed] [Google Scholar]
- Molina JM, Chêne G, Ferchal F, et al. The ALBI trial: A randomized controlled trial comparing stavudine plus didanosine with zidovudine plus lamivudine and a regimen alternating both combinations in previously untreated patients infected with human immunodeficiency virus. J Infect Dis 1999 ; 180 : 351–358. [CrossRef] [PubMed] [Google Scholar]
- Picard V, Angelini E, Maillard A, et al. Comparison of genotypic and phenotypic resistance patterns of human immunodeficiency virus type 1 isolates from patients treated with stavudine and didanosine or zidovudine and lamivudine. J Infect Dis 2001 ; 184 : 781–784. [CrossRef] [PubMed] [Google Scholar]
- Molina JM, Levy Y, Fournier I, et al. Interleukin-2 before antiretroviral therapy in patients with HIV infection: A randomized trial (ANRS 119). J Infect Dis 2009 ; 200 : 206–215. [CrossRef] [PubMed] [Google Scholar]
- Guedj J, Thiébaut R, Commenges D. Maximum likelihood estimation in dynamical models of HIV. Biometrics 2007 ; 63 : 1198–1206. [CrossRef] [PubMed] [Google Scholar]
- Prague M, Commenges D, Drylewicz J, et al. Treatment monitoring of HIV-infected patients based on mechanistic models. Biometrics 2012 ; 68 : 902–911. [CrossRef] [PubMed] [Google Scholar]
- Iyengar R, Zhao S, Chung S-W, et al. Merging systems biology with pharmacodynamics. Sci Transl Med 2012 ; 4 : 126ps7. [CrossRef] [PubMed] [Google Scholar]
Liste des figures
 |
Figure 1. Modèle d’infection par le VIH. dT : variation du nombre ou de la concentration de lymphocytes T CD4+ ; dt : intervalle de temps ; λ : taux de production de cellules de novo ; µ : taux de mortalité des cellules ; T : nombre de cellules présentes ; I : nombre de cellules infectées ; V : nombre de virions circulants ; k : taux d’infection (infectivité) ; dV : variation du nombre de virions ; pI : nombre de virions produits ; p : taux de production par cellules ; c : clairance du virus. |
| Dans le texte | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




