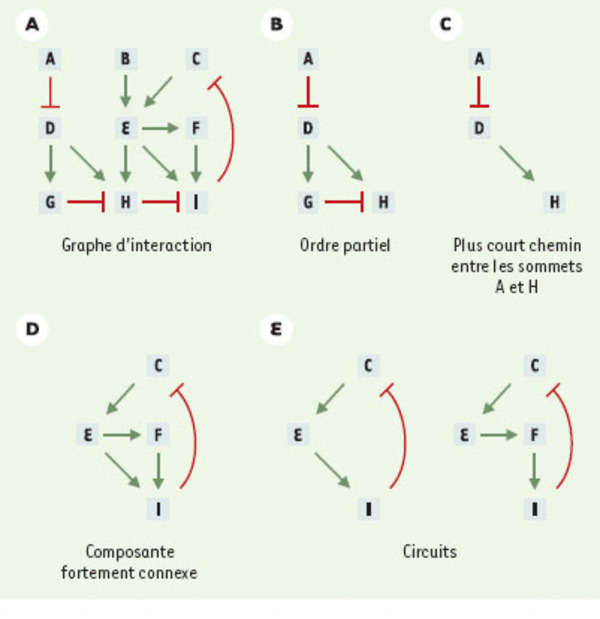
Illustration de quelques notions de la théorie des graphes. A. Exemple de graphe d’interactions complexe. Il est possible d’extraire de ce graphe plusieurs sous-graphes. B. Sous-graphe présentant un ordre partiel. C. Sous-graphe présentant le plus court chemin entre deux sommets. D. Composante fortement connexe : partant d’un élément, il existe au moins un cycle qui ramène vers cet élément. E. Cycle orienté : il s’agit d’un type particulier de composante fortement connexe qui ne possède qu’un seul cycle. Les arcs se terminant par une flèche représentent des activations, les arcs terminés par un trait perpendiculaire représentent des inhibitions impliquant les gènes A à I.