| Numéro |
Med Sci (Paris)
Volume 27, Numéro 2, Février 2011
Représentation en sciences du vivant
|
|
|---|---|---|
| Page(s) | 208 - 213 | |
| Section | Forum | |
| DOI | https://doi.org/10.1051/medsci/2011272208 | |
| Publié en ligne | 8 mars 2011 | |
Vers un patient numérique personnalisé pour le diagnostic et la thérapie guidés par l’image
Représentation en sciences du vivant (5)
Towards a personalized digital patient for diagnosis and therapy guided by image
Inria Sophia Antipolis-Méditerranée, équipe-projet de recherche Asclepios, 2004, route des Lucioles, BP 93, 06902 Sophia Antipolis Cedex, France
*
nicholas.ayache@sophia.inria.fr
Les progrès récents de l’informatique et de l’imagerie médicale permettent de concevoir de nouveaux modèles numériques et personnalisés du patient, au service de la médecine. Ces modèles, dont les paramètres sont optimisés pour s’ajuster aux images acquises in vivo, de la cellule au corps entier, visent à mieux quantifier les observations (aide au diagnostic), à simuler l’évolution d’une pathologie (aide au pronostic), à planifier et simuler une intervention à l’avance pour en optimiser les effets (aide à la thérapie), et à répondre ainsi à certains des enjeux majeurs de la médecine du xxie siècle.
Abstract
Recent advances in computer science and medical imaging allow the design of new computational models of the patient which are used to assist physicians. These models, whose parameters are optimized to fit in vivo acquired images, from cells to an entire body, are designed to better quantify the observations (computer aided diagnosis), to simulate the evolution of a pathology (computer aided prognosis), to plan and simulate an intervention to optimize its effects (computer aided therapy), therefore addressing some of the major challenges of medicine of 21st century.
© 2011 médecine/sciences - Inserm / SRMS
Après la découverte des rayons X à la fin du xixe siècle, le xxe siècle a connu le développement spectaculaire des technologies d’imagerie du corps humain in vivo. Les quatre principales modalités d’imagerie volumique actuellement utilisées de façon courante en clinique (IRM [imagerie par résonance magnétique], scanner X, échographie, médecine nucléaire [23] fournissent des informations sur l’anatomie (la forme) et la physiologie (le fonctionnement) des organes du corps humain. Ces informations peuvent être complétées par une myriade de signaux biomédicaux et de modalités d’imagerie complémentaires dont la liste ne cesse de s’allonger (par exemple la microscopie confocale fibrée que nous illustrerons plus loin) et qui offrent une large gamme de résolutions spatiales (de quelques millimètres au micron) et temporelles (de quelques secondes à la milliseconde). Ces informations sont si riches qu’il est difficile de les analyser globalement et quantitativement sans l’aide de l’informatique.
C’est une des raisons pour lesquelles de nombreux logiciels d’aide à l’analyse des images médicales ont été développés depuis plus d’une trentaine d’années [1–4]. La plupart de ces logiciels s’appuient sur des modèles plus ou moins complexes des images observées qui prennent progressivement en compte une modélisation explicite de l’anatomie et de la physiologie du patient. Durant la même période, des progrès importants ont été réalisés pour simuler avec des modèles mathématiques et informatiques le fonctionnement du vivant, à des échelles allant des gènes à la cellule, et de la cellule au corps entier [5]. Or cette seconde catégorie de modèles [6, 7] simule le vivant à une échelle qui est compatible avec les images médicales et rend possible une confrontation précise entre simulations et observations, dans le but d’ajuster les paramètres des modèles afin qu’ils reproduisent le plus fidèlement possible les images du patient considéré. On peut ainsi transformer des modèles génériques du vivant en modèles personnalisés du corps humain, simulant l’anatomie et la physiologie d’un patient spécifique [8].
Un modèle numérique ainsi personnalisé est beaucoup plus puissant pour interpréter les images médicales du patient ; ses paramètres permettent de quantifier des données anatomiques et physiologiques très utiles au diagnostic. Par ailleurs, un tel modèle, une fois ses paramètres ajustés aux images du patient à un instant donné, peut simuler l’évolution future d’une pathologie, planifier et simuler de façon suffisamment réaliste une intervention afin d’en optimiser les effets et assister ainsi la thérapie. Ces différentes possibilités sont illustrées par la Figure 1.
Une propriété essentielle de ces modèles numériques du patient est leur caractère multi-niveaux : ils présentent généralement :
- un niveau géométrique destiné à capturer la forme des organes, ou par exemple l’extension et le volume de lésions ;- un niveau statistique, pour modéliser une représentation moyenne de l’anatomie ou de la physiologie, détecter un écart par rapport à la normale, et différencier une population de patients d’une population de sujets sains ;
- un niveau biophysique ou biochimique, pour intégrer des propriétés mécaniques ou électriques permettant de simuler une déformation, un écoulement, une activité électrique, etc ;
- et un niveau fonctionnel, pour décrire de façon plus globale l’état d’un organe ou d’un système d’organes (par exemple la nature isovolumique ou isotonique d’une contraction musculaire, la nature avasculaire ou vasculaire d’une croissance tumorale, etc.). Il faut noter que cette liste est loin d’être exhaustive, et que les différents niveaux du modèle sont généralement couplés entre eux. Enfin, chaque niveau peut être multi-échelles pour s’adapter à la résolution variable des images médicales disponibles.
Nous illustrons ces différents niveaux par quatre exemples de modèles récemment développés par notre équipe de recherche avec des partenaires académiques, cliniques et industriels.
Variabilité de l’anatomie
En exploitant des bases de données d’images médicales correspondant à un organe et à des populations choisies (groupes de sujets sains et de patients), il est possible de construire une représentation statistique de certaines structures anatomiques afin de décrire une représentation moyenne ainsi que les variations normales ou pathologiques autour de celle-ci. Ces informations sont généralement essentielles pour construire le premier niveau de description du patient numérique. C’est un sujet d’étude en plein essor, baptisé anatomie algorithmique [9].
La principale difficulté consiste à définir des structures géométriques identifiables et stables (appelées primitives) entre les individus, à les extraire automatiquement des images, puis à calculer des distributions statistiques sur ces primitives. Pour calculer rigoureusement ces distributions, il faut définir des distances adaptées à la nature des espaces mathématiques dans lesquels sont définies ces primitives, ainsi que les transformations géométriques qui permettent de superposer les images de différents sujets dans un référentiel commun.
Dans le cadre d’une collaboration avec le laboratoire LONI de l’Université de Californie (UCLA, Los Angeles, États-Unis), nous avons ainsi développé les outils informatiques et mathématiques permettant de quantifier la variabilité anatomique du cortex cérébral à partir d’une grande base de données d’images par résonance magnétique (IRM) de la tête (Figure 2). Ces modèles géométriques et statistiques du cortex peuvent être ensuite utilisés pour mieux normaliser des études de groupe réalisées en imagerie fonctionnelle1 par exemple, ou bien pour mieux guider la superposition sur un atlas numérique afin d’étiqueter automatiquement le nom des structures anatomiques visibles dans l’image d’un patient [10].
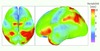 |
Figure 2 Variabilité anatomique du cortex cérébral calculée sur une base d’images par résonance magnétique de 100 sujets normaux, après normalisation affine du cerveau. Les couleurs chaudes correspondent à une plus grande variabilité que les couleurs froides (d’après [10]) ; collaboration avec UCLA, Los Angeles, États-Unis). |
Grâce à une collaboration avec l’hôpital Sainte-Justine (Montréal, Canada), nous avons développé de nouveaux modèles géométriques et statistiques de la colonne vertébrale permettant d’analyser la forme de celle-ci dans une base de données d’images radiologiques de patients scoliotiques ; ces modèles permettent de mieux quantifier l’évolution de la maladie et l’efficacité d’une thérapie [11].
Croissance de tumeurs cérébrales
Pour modéliser la croissance de tumeurs cérébrales, il est nécessaire d’inclure des niveaux de modélisation supplémentaires.
Un premier niveau géométrique et statistique, construit à partir d’une IRM anatomique du patient et d’une image moyenne de patients (atlas), inclut un maillage2 comprenant le volume de la matière grise, de la matière blanche, du liquide céphalo-rachidien, de la faux du cerveau et du crâne du patient. Une IRM de diffusion (moyenne ou du patient) permet d’inclure la direction des principaux faisceaux de fibres de matière blanche qui jouent ensuite un rôle important dans les niveaux suivants [23].
Le second niveau est biomécanique : il décrit une loi de comportement biomécanique des tissus de la tête et calcule sur le maillage du niveau précédent les déformations du cerveau en présence des contraintes appliquées grâce à une méthode de calcul numérique dite « par éléments finis ».
Le troisième niveau est physiopathologique : la densité moyenne de cellules tumorales dans chaque élément de volume évolue selon une équation différentielle de réaction-diffusion qui modélise à la fois une prolifération des cellules tumorales (loi logistique) et leur migration (diffusion anisotrope dans la direction privilégiée des faisceaux de fibres de matière blanche). De plus, la prolifération des cellules tumorales exerce une contrainte locale sur les tissus qui entraîne une déformation du cerveau calculée par le modèle biomécanique du niveau précédent.
La Figure 3 illustre la modélisation de la croissance de tumeurs chez un patient spécifique. Bien que relativement simple, ce modèle macroscopique permet de reproduire la nature très accidentée du front de la tumeur grâce à la prise en compte de la migration privilégiée des cellules tumorales le long des faisceaux de fibres de matière blanche. Mieux, nous avons montré chez un petit nombre de patients [13] qu’une méthode itérative permettait d’ajuster progressivement les paramètres de ce modèle sur une séquence temporelle d’au moins deux images du patient. Les paramètres du modèle ainsi personnalisé (taux de prolifération, vitesse de diffusion dans la matière blanche ou grise, origine spatiale de la tumeur) nous renseignent de façon quantitative sur la dynamique de la croissance tumorale. De plus, ils permettent de simuler son évolution future, en prenant éventuellement en compte la thérapie choisie (chirurgie, radiothérapie, chimiothérapie). Enfin, le modèle numérique permet de prédire l’extension de la tumeur au-delà de sa frontière visible sur l’IRM du dernier examen et permettrait donc de redéfinir de façon plus précise les marges de sécurité définies en radiothérapie et en neurochirurgie, en prenant en compte la spécificité de la tumeur et l’anatomie de chaque patient [14] (collaboration avec la Harvard medical school et le Centre Antoine Lacassagne de Nice).
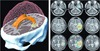 |
Figure 3 Modèle de croissance de tumeurs cérébrales. À gauche, le maillage par éléments finis qui permet de simuler l’évolution de la tumeur ; à droite, le modèle est initialisé dans les images acquises au premier examen (première colonne), pour simuler l’évolution de la tumeur sur une période de six mois (seconde colonne), qui peut être comparée aux images du patient lors du second examen (troisième colonne). Collaboration avec la Harvard medical school (Boston, États-Unis) et le Centre Antoine Lacassagne (Nice, France) (d’après [12]). |
Fonction cardiaque
Pour décrire le fonctionnement électromécanique du cœur, un modèle numérique encore plus complexe a été développé en partenariat avec plusieurs équipes [15, 16]. Ce modèle est également multi-niveaux (Figure 4).
 |
Figure 4 Modèle électromécanique des ventricules cardiaques. Au centre, le modèle numérique simule l’activité électrique et mécanique des ventricules cardiaques d’un patient. La couleur représente le potentiel d’action moyen des tissus dans un élément de volume, et les petites flèches bleues le mouvement des tissus. Le modèle est personnalisé grâce aux images anatomiques et dynamiques et à des mesures électrophysiologiques réalisées in vivo sur le patient (à gauche et à droite). Collaboration avec King’s College (KCL) et Saint-Thomas Hospital (Londres), ainsi que Philips et Siemens (d’après [16]). |
Un premier niveau géométrique et statistique consiste à ajuster automatiquement un maillage à l’anatomie réelle des ventricules gauche et droit (VG, VD) observés sur les IRM anatomiques du patient. Un atlas statistique des principaux faisceaux de fibres cardiaques est ajusté à ce maillage.
Le second niveau est électrique : le potentiel d’action (différence de potentiel extra et intracellulaire) moyenné sur un élément de volume du maillage précédent évolue selon une équation différentielle de réaction-diffusion qui privilégie une propagation plus rapide dans la direction des fibres cardiaques que dans le plan transverse.
Le troisième niveau est mécanique : le muscle cardiaque y est décrit comme un matériau contractile au comportement viscoélastique non linéaire. La contraction puis la relaxation active des fibres sont contrôlées par le potentiel d’action calculé au second niveau. L’ensemble est décrit par un système d’équations différentielles qui permet de simuler le mouvement des sommets du maillage du cœur.
Un quatrième niveau est nécessaire pour décrire les grandes phases physiologiques du cœur et les conditions aux limites associées. Lorsque les valves des ventricules sont fermées, la contraction ou la relaxation des ventricules est isovolumique ; sinon, une condition de pression réaliste est appliquée uniformément sur l’endocarde des deux ventricules. L’onde de pression cardiaque est simulée sur l’aorte et les artères pulmonaires.
Ici encore, le modèle, bien que relativement simple, permet de simuler un mouvement réaliste du cœur, reproduisant notamment le mouvement de torsion caractéristique du muscle. La personnalisation des paramètres électriques (principalement la conductivité locale) et mécaniques (principalement la contractilité locale du myocarde) sur des zones correspondant à des territoires vasculaires est encore un sujet de recherche actif, mais des premiers résultats prometteurs sont obtenus à partir de méthodes itératives qui comparent les simulations électriques et mécaniques aux observations (images IRM et électrophysiologie 3D) et font évoluer progressivement les paramètres des modèles pour rapprocher simulations et observations à chaque itération [17, 18].
Un modèle cardiaque ainsi personnalisé (Figure 4) permettra de prédire le bénéfice attendu de différentes thérapies, notamment de l’ablation radiofréquence de tissus cardiaques pour traiter certains troubles du rythme. Il permettra également d’évaluer le bénéfice potentiel d’une resynchronisation cardiaque par la pose d’un pacemaker [19] ainsi qu’une meilleure optimisation de son implantation et du réglage de ses paramètres, alors qu’aujourd’hui encore 30 à 40 % des patients ne présentent pas d’amélioration de la fonction cardiaque après cette intervention (collaboration avec l’hôpital Saint-Thomas de Londres, les équipes INRIA Macs, Reo et Sysiphe, ainsi que Philips et Siemens).
L’imagerie microscopique in vivo
Les modèles précédents sont macroscopiques, ils simulent le fonctionnement du vivant à des échelles compatibles avec les modalités d’imagerie classiques utilisées en pratique clinique. Avec l’introduction en clinique de nouvelles modalités d’imagerie microscopique (microscopie confocale fibrée3) dont la résolution proche du micron permet de visualiser l’architecture cellulaire des tissus, de nouveaux modèles doivent être introduits [20]. Nous avons par exemple participé au développement d’un logiciel de construction de mosaïques d’images qui combine le mouvement de la sonde d’acquisition avec un modèle de déplacement et de déformations des tissus, pour élargir de façon très significative le champ de vision tout en augmentant artificiellement la résolution de l’image (principe de la super-résolution) [21]. Cette approche permettra de relier des modèles incluant des échelles microscopiques avec des échelles mésoscopiques. Nous développons également un nouveau concept d’atlas d’images microscopiques qui, à partir d’une grande base de données, fournit les images annotées les plus proches visuellement des images spécifiques auxquelles est confronté le médecin lors de l’examen d’un nouveau patient [22]. Ces deux avancées sont illustrées dans la Figure 5 (collaboration avec Mauna Kea Technologies à Paris et la Mayo Clinic de Jacksonville aux États-Unis).
 |
Figure 5 Atlas numérique « intelligent ». Une image microscopique d’un polype bénin acquise in vivo pendant une coloscopie est soumise au système (cadre bleu) : le logiciel fournit automatiquement (première ligne) les 4 images les plus similaires de la base de données (atlas d’images microscopiques), toutes bénignes, avec le diagnostic préalablement enregistré par des experts. Idem pour un polype patho logique (cadre rouge) et les 4 images les plus similaires (seconde ligne), toutes pathologiques. Collaboration avec Mauna Kea Technologies (Paris, France) et Mayo Clinic (Jacksonville, États-Unis) (d’apres [22]). |
Conclusion
Cet article a montré quelques-unes des perspectives nouvelles qu’offrent l’analyse et la simulation informatiques des images médicales pour assister le diagnostic et la thérapie. Si certains modèles numériques personnalisés du patient sont déjà utilisés en clinique (notamment des modèles purement géométriques, très utilisés pour fusionner des images provenant de modalités différentes et pour la visualisation 3D), il reste encore des problèmes difficiles à résoudre (notamment l’identification automatique des paramètres de modèles plus complexes, incluant des niveaux statistiques, biophysiques et biochimiques) et beaucoup de validation à effectuer en collaboration étroite avec des cliniciens pour généraliser leur utilisation. Mais on peut déjà anticiper qu’en s’ajustant aux images in vivo du patient, ces nouveaux modèles numériques et personnalisés permettront progressivement d’assister de façon généralisée la médecine du xxie siècle.
Conflit d’intérêts
Les auteurs déclarent n’avoir aucun conflit d’intérêts concernant les données publiées dans cet article.
Remerciements
Les auteurs tiennent à remercier tous les membres de l’équipe de recherche Asclepios de l’INRIA ainsi que tous les collaborateurs académiques, cliniques et industriels dont les travaux sont rapportés ici.
Elle est fondée sur le principe de la microscopie confocale qui permet d’obtenir une imagerie microscopique à différents niveaux de profondeur. Le procédé utilise, à la place de l’objectif du microscope, un faisceau de fibres optiques à l’intérieur d’une sonde (de diamètre de l’ordre du millimètre). Chacune de ces microfibres est parcourue à un instant donné par le faisceau laser selon un mode de balayage très rapide. Ce faisceau laser va illuminer le tissu, et les fibres vont, dans le même temps, recueillir la fluorescence émise par celui-ci en quelques nanosecondes.
Références
- Duncan J, Ayache N. Medical image analysis: progress over two decades and the challenges ahead. IEEE Trans Pattern Anal Mach Intell 2000 ; 22 : 85-106. [CrossRef] [Google Scholar]
- Ayache N (ed). Computer vision, virtual reality and robotics in medicine. First international conference on computer vision, virtual reality and robotics in medicine, CVRMed’95. Lecture notes in computer science Berlin-Heidelberg : Springer-Verlag, 1995 : 568 p. [Google Scholar]
- Ayache N, Ourselin S, Maeder A. (eds). Medical image computing and computer-assisted intervention (MICCAI). Lecture notes in computer science, Berlin-Heidelberg : Springer-Verlag, 2007 : 1002 p. [Google Scholar]
- Ayache N, Delingette H, Sermesant M (eds). Functional imaging and modeling of the heart (FIMH). Lecture notes in computer science, Berlin-Heidelberg : Springer-Verlag : 2009, 538 p. [Google Scholar]
- Hunter PJ, Borg TK. Integration from proteins to organs: the physiome project. Nat Rev Mol Cell Biol 2003 ; 4 : 237-243. [CrossRef] [PubMed] [Google Scholar]
- Ayache N. (ed). Computational models for the human body In: Ciarlet P. ed. Handbook of numerical analysis. Amsterdam : Elsevier, 2004 : 670 p. [Google Scholar]
- Ayache N, Delingette H (eds). Surgery simulation and soft tissue modeling. Lecture notes in computer science. Berlin-Heidelberg : Springer-Verlag, 2003 : 386 p. [Google Scholar]
- Ayache N, Clatz O, Delingette H, et al. Asclepios: a research project-team at INRIA for the analysis and simulation of biomedical images. In : Bertot Y, Huet G, Lévy JJ, Plotkin G, eds. From semantics to computer science: essays in honor of Gilles Kahn. Cambridge : Cambridge University Press, 2009 : 415-436. [CrossRef] [Google Scholar]
- Pennec X, Joshi S (eds). Mathematical foundations of computational anatomy. Geometrical and statistical methods for modelling biological shape variability. 2006. http://www-sop.inria.fr/asclepios/Publications/Xavier.Pennec/MFCA06.pdf. [Google Scholar]
- Fillard P, Arsigny V, Pennec X, et al. Measuring brain variability by extrapolating sparse tensor fields measured on sulcal lines. Neuroimage 2007 ; 34 : 639-650. [CrossRef] [PubMed] [Google Scholar]
- Boisvert J, Cheriet F, Pennec X, et al. Geometric variability of the scoliotic spine using statistics on articulated shape models. IEEE Trans Med Imaging 2008 ; 27 : 557-568. [CrossRef] [PubMed] [Google Scholar]
- Clatz O, Sermesant M, Bondiau PY, et al.. Realistic simulation of the 3D growth of brain tumors in MR images coupling diffusion with mass effect. IEEE Trans Med Imaging 2005 ; 24 : 1334-1346. [CrossRef] [PubMed] [Google Scholar]
- Konukoglu E, Clatz O, Menze BH, et al. Image guided personalization of reaction-diffusion type tumor growth models using modified anisotropic eikonal equations. IEEE Trans Med Imaging 2010 ; 29 : 77-95. [CrossRef] [PubMed] [Google Scholar]
- Konukoglu E, Clatz O, Bondiau PY, et al. Extrapolating glioma invasion margin in brain magnetic resonance images: suggesting new irradiation margins. Med Image Anal 2010 ; 14 : 111-125. [CrossRef] [PubMed] [Google Scholar]
- Sainte-Marie J, Chapelle D, Cimrman R, Sorine M. Modeling and estimation of the cardiac electromechanical activity. Computers Structures 2006 ; 84 : 1743-1759. [CrossRef] [Google Scholar]
- Sermesant M, Delingette H, Ayache N. An electromechanical model of the heart for image analysis and simulation. IEEE Trans Med Imaging 2006 ; 25 : 612-625. [CrossRef] [PubMed] [Google Scholar]
- Billet F, Sermesant M, Delingette H, Ayache N. Cardiac motion recovery and boundary conditions estimation by coupling an electromechanical model and cine-MRI data. In : Ayache N, Delingette H, Sermesant M eds. Proceedings of functional imaging and modeling of the heart 2009 (FIMH 09). Lecture notes in computer science Berlin-Heidelberg : Springer-Verlag, 2009 : 376-385. [Google Scholar]
- Mansi T, André B, Lynch M. Virtual pulmonary valve replacement interventions with a personalized cardiac electromechanical model. Recent advances in the 3D physiological human. In : Ayache N, Ayache N, Delingette H, Sermesant M, eds. Proceedings of functional imaging and modeling of the heart 2009 (FIMH 09). Lecture notes in computer science. Berlin-Heidelberg : Springer-Verlag, 2009 : 201-210. [Google Scholar]
- Sermesant M, Billet F, Chabiniok R, et al. Personalized electromechanical model of the heart for the prediction of the acute effects of cardiac resynchronisation therapy. In : Ayache N, Delingette H, Sermesant M, eds. Proceedings of functional imaging and modeling of the heart 2009 (FIMH 09). Lecture notes in computer science. Berlin-Heidelberg : Springer-Verlag, 2009 : 239-248. [Google Scholar]
- Vercauteren T, Ayache N, Savoire N, et al. Processing of in vivo fibered confocal microscopy video sequences. In : Rittscher J, Machiraju R, Wong STC, eds. Microscopic image analysis for life science applications. Boston (London) : Artech House, 2008 : 441-463. [Google Scholar]
- Vercauteren T, Perchant A, Malandain G, et al. Robust mosaicing with correction of motion distortions and tissue deformation for in vivo fibered microscopy. Med Image Anal 2006 ; 10 : 673-692. [CrossRef] [PubMed] [Google Scholar]
- André B, Vercauteren T, Wallace MB, et al. Endomicroscopic video retrieval using mosaicing and visual words. In : Proceedings of the seventh IEEE International symposium on biomedical imaging 2010 (ISBI’10) 2010 ; 1419-1422. [CrossRef] [Google Scholar]
- Coatrieux JL, Velut J, Dillenseger JL, Toumoulin C. De l’imagerie médicale à la thérapie guidée par l’image. Med Sci (Paris) 2010 ; 26 : 1103-1109. [CrossRef] [EDP Sciences] [PubMed] [Google Scholar]
Liste des figures
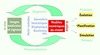 |
Figure 1 Vers un patient numérique personnalisé (d’après [4]). |
| Dans le texte | |
 |
Figure 2 Variabilité anatomique du cortex cérébral calculée sur une base d’images par résonance magnétique de 100 sujets normaux, après normalisation affine du cerveau. Les couleurs chaudes correspondent à une plus grande variabilité que les couleurs froides (d’après [10]) ; collaboration avec UCLA, Los Angeles, États-Unis). |
| Dans le texte | |
 |
Figure 3 Modèle de croissance de tumeurs cérébrales. À gauche, le maillage par éléments finis qui permet de simuler l’évolution de la tumeur ; à droite, le modèle est initialisé dans les images acquises au premier examen (première colonne), pour simuler l’évolution de la tumeur sur une période de six mois (seconde colonne), qui peut être comparée aux images du patient lors du second examen (troisième colonne). Collaboration avec la Harvard medical school (Boston, États-Unis) et le Centre Antoine Lacassagne (Nice, France) (d’après [12]). |
| Dans le texte | |
 |
Figure 4 Modèle électromécanique des ventricules cardiaques. Au centre, le modèle numérique simule l’activité électrique et mécanique des ventricules cardiaques d’un patient. La couleur représente le potentiel d’action moyen des tissus dans un élément de volume, et les petites flèches bleues le mouvement des tissus. Le modèle est personnalisé grâce aux images anatomiques et dynamiques et à des mesures électrophysiologiques réalisées in vivo sur le patient (à gauche et à droite). Collaboration avec King’s College (KCL) et Saint-Thomas Hospital (Londres), ainsi que Philips et Siemens (d’après [16]). |
| Dans le texte | |
 |
Figure 5 Atlas numérique « intelligent ». Une image microscopique d’un polype bénin acquise in vivo pendant une coloscopie est soumise au système (cadre bleu) : le logiciel fournit automatiquement (première ligne) les 4 images les plus similaires de la base de données (atlas d’images microscopiques), toutes bénignes, avec le diagnostic préalablement enregistré par des experts. Idem pour un polype patho logique (cadre rouge) et les 4 images les plus similaires (seconde ligne), toutes pathologiques. Collaboration avec Mauna Kea Technologies (Paris, France) et Mayo Clinic (Jacksonville, États-Unis) (d’apres [22]). |
| Dans le texte | |
Les statistiques affichées correspondent au cumul d'une part des vues des résumés de l'article et d'autre part des vues et téléchargements de l'article plein-texte (PDF, Full-HTML, ePub... selon les formats disponibles) sur la platefome Vision4Press.
Les statistiques sont disponibles avec un délai de 48 à 96 heures et sont mises à jour quotidiennement en semaine.
Le chargement des statistiques peut être long.




