| Numéro |
Med Sci (Paris)
Volume 21, Numéro 5, Mai 2005
|
|
|---|---|---|
| Page(s) | 530 - 534 | |
| Section | M/S revues | |
| DOI | https://doi.org/10.1051/medsci/2005215530 | |
| Publié en ligne | 15 mai 2005 | |
Simulation numérique du système cardiovasculaire
Numerical simulation of the cardiovascular system
INRIA, Projet REO, Domaine de Voluceau-Rocquencourt, BP 105, 78153 Le Chesnay Cedex, France
*
jean-frederic.gerbeau@inria.fr
Les progrès réalisés en mathématiques appliquées permettent aujourd’hui d’envisager la simulation sur ordinateur de certains compartiments du système cardiovasculaire. Nous proposons de faire un point sur quelques modèles, en nous focalisant sur la simulation de l’écoulement du sang dans des artères déformables et sur la simulation de la contraction du myocarde sous l’effet de la propagation d’un signal électrique. Nous tentons également de présenter des applications possibles de ce type de travaux.
Abstract
In this article, we aim at giving a non-technical overview of some mathematical models currently used in the numerical simulation of the cardiovascular system. A hierarchy of models for blood flows in large arteries is briefly described as well as an electromechanical model for the heart. We discuss some possible applications of the numerical simulations of such models, for example the optimization of prostheses. We also address the issue of the data assimilation for the calibration of the models.
© 2005 médecine/sciences - Inserm / SRMS
Dans cet article, nous souhaitons présenter, de manière non technique, des travaux récents sur la simulation numérique du système cardiovasculaire. Le terme simulation couvre des notions tellement différentes qu’il n’est peut-être pas inutile de commencer par préciser le sens qu’on lui donne ici. Une simulation numérique est la résolution sur ordinateur d’équations mathématiques qui modélisent un phénomène. La discipline qui s’intéresse à la simulation numérique est une branche des mathématiques appliquées, appelée calcul scientifique. En amont de la simulation se déroule la phase de modélisation, c’est-à-dire la mise en équations du problème. Suivent la phase d’analyse mathématique, dont le but est d’établir les propriétés des équations, puis le développement et l’analyse de méthodes numériques. Une fois ces méthodes programmées, il est alors possible de réaliser sur ordinateur des expériences numériques qui permettent d’enrichir les expériences in vivo et in vitro. Naturellement, des allers retours sont nécessaires entre ces diverses phases.
Hiérarchie de modèles pour la circulation artérielle
Modèles sans dépendance spatiale
Les modèles les plus simples d’écoulements sanguins décrivent l’évolution dans le temps du débit et de la pression moyenne dans un compartiment vasculaire entier, sur la base de considérations hydrauliques élémentaires. Les équations sous-jacentes sont simples : il s’agit d’équations différentielles ordinaires, c’est-à-dire reliant des fonctions d’une seule variable (le temps) et leurs dérivées.
On utilise souvent une analogie électrique pour décrire ces modèles : le débit sanguin et la chute de pression sont représentés respectivement par un courant électrique et une différence de potentiel, les effets dissipatifs liés à la viscosité du sang sont représentés par une résistance, et l’élasticité de la paroi des artères par un condensateur. Le modèle électrique le plus simple d’arbre artériel consiste en une résistance, modélisant l’effet des petites artères, et un condensateur monté en parallèle, modélisant l’élasticité des grosses artères. Il permet d’illustrer le fait que l’énergie élastique accumulée pendant la systole est restituée pendant la diastole (effet Windkessel, mis en évidence dès 1733 par Stephen Hales).
Ces modèles présentent l’intérêt d’être simples mathématiquement et de pouvoir être résolus efficacement sur ordinateur. En contrepartie, les informations qu’ils fournissent sont assez limitées. Ils sont cependant très utilisés pour décrire schématiquement le système circulatoire dans des travaux qui se concentrent sur des modèles de cœur [1], sur la description des boucles de contrôle du système cardiovasculaire [2], ou encore pour décrire sommairement les vaisseaux périphériques quand les gros vaisseaux sont modélisés plus finement.
Modèles unidimensionnels
Les modèles précédents sont inadaptés pour décrire les phénomènes de propagation d’ondes dans le tronc artériel. Or, ces ondes contiennent des informations importantes : l’augmentation de leur vitesse de propagation traduit une diminution de l’élasticité des artères, leur allure est modifiée par les bifurcations, sténoses, endoprothèses…
En considérant une représentation « filaire » des vaisseaux sanguins, la position spatiale d’un point peut être repérée à l’aide d’une seule coordonnée le long de l’axe du vaisseau. Les inconnues, débit et pression moyenne, sont à présent des fonctions de deux variables, le temps et l’espace. Le modèle est donc décrit par des équations aux dérivées partielles. Celles-ci traduisent des principes de conservation de masse et des bilans de quantité de mouvement. Bien que très anciennes (elles ont été proposées par Euler en 1775), leur analyse mathématique et les méthodes pour les résoudre numériquement sont encore des sujets de recherche très actifs.
Ces modèles permettent, par exemple, de représenter les phénomènes de peaking (augmentation de l’amplitude) et steepening (pincement de la largeur) de l’onde de pression qui se propage dans le tronc artériel.
Modèles tridimensionnels
Les modèles décrits ci-dessus ont pour vocation une description globale de la circulation. Mais il peut être intéressant de considérer des phénomènes localisés : où un anévrisme risque-t-il de se rompre ? Pourquoi une zone est-elle un lieu privilégié d’athérosclérose ? Comment diminuer le risque de resténose après une angioplastie ou un pontage ? Autant le dire tout de suite, la simulation numérique ne sait pas encore apporter de réponses complètes à ces questions. Des mécanismes clés - comme le rôle de l’inflammation dans l’athérosclérose ou la capacité de remodelage des parois vasculaires - ne sont pas intégrés dans les modèles qu’on simule. Cependant, des indices laissent espérer que des éléments de réponses puissent être obtenus sur la base de considérations purement mécaniques.
L’hypothèse d’un lien entre les propriétés mécaniques locales de l’écoulement du sang et le développement de l’athérosclérose a été proposée au début des années 1970 [3]. Depuis, de nombreuses études ont confirmé cette hypothèse. Ainsi, un lien entre localisation de l’athérome dans la carotide humaine et zones à faibles contraintes pariétales a été établi [4]. Des mesures in vivo sur des chiens ont montré que les lésions athéromateuses ont tendance à se développer dans les zones où la moyenne temporelle du cisaillement dans la paroi est faible [5]. Il a été également montré que les zones de recirculation et les zones à faible cisaillement offraient des conditions favorables à l’athérosclérose dans les coronaires humaines [6]. Ces conditions d’écoulement seraient en effet propices à l’interaction des lipoprotéines, des monocytes et des plaquettes avec les cellules endothéliales qui tapissent les parois artérielles.
Du point de vue de la modélisation, l’importance des propriétés locales de l’écoulement indique qu’on ne peut se contenter de quantités comme un débit ou une pression moyenne : l’accès au cisaillement ou aux contraintes sur la paroi de l’artère nécessite la connaissance de la vitesse et de la pression en « tout point » et à « tout instant ». Les équations qui fournissent ces quantités sont celles de la mécanique des fluides incompressibles tridimensionnelles, appelées équations de Navier-Stokes. Comme pour les équations des modèles unidimensionnels, leur analyse mathématique et numérique est loin d’être achevée. En outre, la simulation de ces modèles 3D nécessite considérablement plus de puissance de calcul que les modèles précédents et ne peut donc être envisagée que sur quelques portions d’artère.
Pour effectuer des simulations 3D réalistes, il est essentiel de pouvoir utiliser dans les calculs des géométries fournies par l’imagerie médicale. On sait en effet que la forme complexe des vaisseaux engendre des structures d’écoulement différentes de celles observées dans des géométries idéalisées [7].
Pour les grosses artères, le réalisme impose également la prise en compte du déplacement de la paroi des vaisseaux. Ce problème est sensiblement plus difficile que la simulation de l’écoulement dans un conduit rigide et nécessite le développement de nouvelles méthodes numériques [8]. La difficulté vient du fait que deux types de phénomènes physiques interagissent étroitement : la paroi se déforme sous l’effet du passage du sang, et le mouvement de la paroi agit à son tour sur l’écoulement. La Figure 1 montre un exemple de simulation d’interaction fluide/structure lors du passage d’une onde de pression dans un anévrisme [9]. Ces simulations donnent par exemple accès aux contraintes dans la paroi vasculaire.
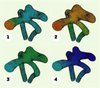 |
Figure 1. Propagation d’une onde de pression dans un anévrisme. Les quatre images représentent la pression dans l’anévrisme à des instants différents (bleu : pression faible, orange : pression forte). Le couplage entre l’écoulement du sang et le déplacement de la paroi artérielle est pris en compte : noter que la paroi de l’anévrisme se déforme, ce qui engendre la propagation de l’onde de pression. La géométrie sur laquelle a été effectuée la simulation provient d’une image médicale. Elle a été « maillée » (triangles noirs) pour permettre d’effectuer le calcul. |
Un intérêt des expériences numériques est de permettre de faire varier les paramètres du modèle bien plus facilement que dans les expériences in vitro ou in vivo. Mieux encore, il existe des techniques mathématiques permettant de faire varier automatiquement ces paramètres pour atteindre un objectif donné. Supposons que l’on dispose d’un modèle de l’écoulement du sang dans un pontage et que l’on ait identifié un critère, impliquant par exemple les contraintes que le sang exerce sur la paroi, favorisant une resténose. On peut alors écrire un algorithme déterminant automatiquement la forme que devrait avoir le pontage pour minimiser les risques de resténose. Des exemples très préliminaires d’une telle démarche ont déjà été proposés [10].
Modélisation, simulation et estimation de l’activité électromécanique du cœur
Contexte et objectifs
Une modélisation globale de la circulation nécessite naturellement - en association avec les modèles d’artères présentés ci-dessus - un modèle du comportement électromécanique du myocarde. Il est possible d’envisager des descriptions assez fines pour que les simulations puissent rendre compte de nombreux phénomènes physiques. Mais une limite vient de ce qu’un modèle fin utilisera un très grand nombre de paramètres qui seront difficiles, voire impossibles à identifier suivant la richesse des mesures in vivo (cinématiques et électriques) disponibles. Il est donc important d’adapter la finesse de la modélisation à la richesse des mesures.
Les diverses mesures in vivo de l’activité cardiaque sont faites avec un échantillonnage spatial et temporel réduit. Il est néanmoins envisageable, en confrontant ces mesures à des simulations de modèles d’une complexité adaptée, d’en tirer plus d’information que celle qui est directement présente dans la mesure elle-même. Il est ainsi possible de construire une sorte de « capteur logiciel », système ayant en entrée les mesures cliniques et permettant d’accéder à des variables ou paramètres non directement mesurés, comme les contraintes ou la contractilité, ou de rendre plus précis certains indicateurs.
Modélisation et simulation
Deux phénomènes physiques principaux doivent être modélisés pour rendre compte du comportement du cœur : la propagation du potentiel d’action dans le tissu et la contraction du muscle cardiaque sous l’effet du potentiel d’action.
Le premier phénomène est de nature électrique, le second de nature mécanique. Dans ce qui suit, nous nous concentrons sur la modélisation développée pour le phénomène mécanique. Pour le potentiel d’action, nous renvoyons le lecteur à [11] et à ses références.
Il est communément admis que les travaux de Huxley sur la dynamique des ponts actine-myosine [12], au niveau microscopique (du sarcomère), permettent d’expliquer les phénomènes de contraction dans le muscle cardiaque. L’étude du mécanisme de formation de ces ponts par une approche multi-échelles, généralisant celle de [13], a permis de développer une loi de comportement au niveau mésoscopique, c’est-à-dire à l’échelle de la myofibre [14], compatible avec le formalisme de Huxley, et résultant de la description du comportement collectif des nanomoteurs moléculaires actine-myosine [15]. Cette loi, permettant de rendre compte du couplage excitation-contraction, s’écrit :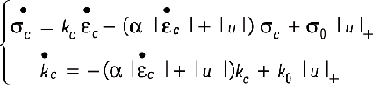
Dans ces équations, un point sur un symbole représente la dérivée par rapport au temps, tandis que | u|+ vaut u lorsque u ≥ 0, et 0 sinon. Ce système est une relation dynamique qui fournit σc, la contrainte contractile, en fonction de εc, la déformation contractile le long du sarcomère. Il s’agit d’une loi de comportement mécanique. Dans cette loi, u représente l’entrée électrique, directement liée au potentiel d’action. La variable intermédiaire kc désigne une « raideur équivalente », alors que σ0 et k0représentent la contractilité du muscle au point considéré.
Une modélisation 3D complète de l’activité mécanique du cœur est obtenue en insérant cette loi de comportement dans un modèle rhéologique, tel que celui de A.V. Hill [16], puis en écrivant les équations d’équilibre de la mécanique des milieux continus [17]. Pour compléter ces équations, il faut aussi prendre en compte le comportement du fluide. Mais il est pour l’instant hors de portée de le faire avec des modèles 3D du type de ceux décrits précédemment pour les artères. On se contente donc d’une modélisation simplifiée sous la forme d’une pression supposée uniforme et d’un volume global par compartiment du myocarde.
Pour réaliser des simulations de ce modèle, il faut disposer d’une description fine de la géométrie de l’organe, avec en particulier la direction privilégiée des fibres musculaires en tout point. Pour les résultats présentés ci-dessous, nous avons utilisé les données anatomiques d’un cœur de chien diffusées par le Bioengineering Institute de l’université d’Auckland (Nouvelle-Zélande). Les directions des fibres sont visualisées dans la Figure 2.
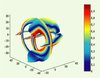 |
Figure 2. Angle des fibres (cosinus) sur 3 coupes orthogonales. La couleur représente la valeur du cosinus de l’angle que présente au point considéré la fibre avec le plan orthogonal à l’axe principal du cœur. On voit que cet angle est maximal près de l’épicarde et de l’endocarde (source : R. Cimrman, INRIA, Rocquencourt). |
La Figure 3 présente des résultats de simulations sous la forme de vues en coupe de l’état de déformation du myocarde à différents moments du cycle cardiaque.
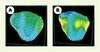 |
Figure 3. Vues en coupe des déformations du myocarde en fin de diastole (A) et de systole (B). Les couleurs représentent l’amplitude des déplacements par rapport à la position de fin de diastole (bleu : plus faible, rouge : plus élevée), et les lignes blanches le maillage de calcul (source : J. Sainte-Marie, INRIA, Rocquencourt). |
Confrontations modèles/mesures
L’intérêt de confronter les modèles (via leurs simulations) aux mesures pour construire un capteur logiciel, véritable outil d’aide au diagnostic, a été développé plus haut. Une telle problématique se retrouve dans beaucoup d’autres domaines où les mesures sont abondantes et complexes, comme en météorologie ou en océanographie, et la démarche qui consiste à « automatiser » le processus de « mise en correspondance » du modèle avec les données est connue sous le nom d’assimilation de données. Différentes méthodes ont été développées pour cela [18].
La Figure 4 montre des résultats préliminaires obtenus avec notre modèle de cœur, sur une géométrie simplifiée. Dans ce cas, nous sommes partis de données synthétiques (c’est-à-dire fournies par la simulation du modèle avec un jeu de paramètres connus) et l’objectif de l’assimilation de données est de chercher à retrouver la valeur des paramètres, qui peut éventuellement être non uniforme dans le tissu. En particulier, on voit qu’on arrive assez bien à estimer la variabilité du paramètre de contractilité, qui peut dans ce cas représenter une zone infarcie. Bien entendu, l’objectif à terme est de pouvoir utiliser de vraies mesures, notamment des images d’IRM ou d’échographie. Des travaux sont en cours dans cette direction [19].
 |
Figure 4. Résultat de l’assimilation sur σ0. Les couleurs représentent les valeurs du paramètre (bleu pour une contractilité anormalement faible). Les résultats obtenus par la procédure d’assimilation (B) sont en bonne adéquation avec les valeurs de référence (A) ayant servi à engendrer les données synthétiques (source : J. Sainte-Marie, INRIA, Rocquencourt). |
Conclusions
Nous avons tenté de donner un bref aperçu des possibilités actuelles de la simulation numérique du système cardiovasculaire. Même si des avancées significatives ont été réalisées ces dernières années, reconnaissons que les applications concrètes sont encore balbutiantes. Mais le potentiel à moyen terme est considérable : un modèle convenablement choisi doit permettre d’améliorer la compréhension du fonctionnement du système cardiovasculaire sain ou malade, voire de simuler à des fins d’évaluation et d’aide à la décision l’impact de stratégies thérapeuthiques. En outre, en confrontant de manière automatisée les résultats de simulations à des mesures cliniques, on peut construire un véritable capteur logiciel capable de donner accès à des variables ou paramètres cachés, et donc d’apporter une aide au diagnostic.
Remerciements
Dominique Chapelle est directeur de recherche à l’INRIA, responsable du projet MACS. Jean-Frédéric Gerbeau est chargé de recherche à l’INRIA, responsable du projet REO. L’essentiel des travaux récents décrits dans cet article a été réalisé dans le cadre d’un projet européen intitulé HAEMODEL (http://mox.polimi.it/it/progetti/haemodel/) et d’une action de recherche collaborative intitulée ICEMA2 (http://wwwrocq.inria.fr/sosso/icema2/icema2.html) associant diverses équipes de l’INRIA et des partenaires d’autres organismes.
Références
- Segers P, Stergiopulos N, Westerhof N, et al. Systemic and pulmonary hemodynamics assessed with a lumped-parameter heart-arterial interaction model. J Engin Mathematics 2003; 14 : 185–99. [Google Scholar]
- Monti A, Médigue C, Sorine M. Short-term control of the cardiovascular system : modelling and signal analysis. Rapport de recherche INRIA n° 4427. Paris : INRIA, 2002. [Google Scholar]
- Caro CG, Fitz-Gerald JM, Schroter RC. Atheroma and aterial wall shear : observation, correlation and proposal of a shear dependant mass transfer mechanism for atherogenesis. Proc R Soc Lond B Biol Sci 1971; 177 : 109–59. [Google Scholar]
- Zarins CK, Giddens DP, Bharadvaj BK, et al. Carotid bifurcation atherosclerosis : quantitative correlation of plaque localization with flow velocity profiles and wall shear stress. Circ Res 1983; 53 : 502–14. [Google Scholar]
- Yamamoto T, Tanaka H, Jones CJH, et al. Blood velocity profiles in the origin of the canine renal-artery and their relevance in the localization and development of atherosclerosis. Arterioscler Thromb 1992; 12 : 626–32. [Google Scholar]
- Asakura T, Karino T. Flow patterns and spatial distribution of atherosclerotic lesions in human coronary arterie. Circ Res 1990; 66 : 1045–66. [Google Scholar]
- Botnar R, Rappitsch G, Scheidegger MB, et al. Hemodynamics in the carotid artery bifurcation : a comparison between numerical simulations and in vitro MRI measurements. J Biomec 2000; 33 : 137–44. [Google Scholar]
- Gerbeau JF, Vidrascu M. A quasi-Newton algorithm based on a reduced model for fluid-structure interaction problems in blood flows. Math Model Num Anal 2003; 37 : 663–80. [Google Scholar]
- Gerbeau JF, Vidrascu M, Frey P. Fluid-structure interaction in blood flows on geometries coming from medical imaging. Comput Struct 2005; 83 : 155-65 (accessible sur http://www.sciencedirect.com/science/journal/00457949). [Google Scholar]
- Quarteroni A, Rozza G. Optimal control and shape optimization in aorto-coronaric bypass anastomoses. Math Models Meth Appl Sci 2003; 13 : 1801–23. [Google Scholar]
- Panfilov AV, Holden AV. Computational biology of the heart. Chichester : John Wiley and Sons, 1997. [Google Scholar]
- Huxley AF. Muscle structure and theories of contraction. In : Progress in biophysics and biological chemistry, vol. 7, chapter 6. Oxford : Pergamon Press, 1957. [Google Scholar]
- Zahalak GI. A distribution moment approximation for kinetic theories of muscular contraction. Math Biosci 1981; 55 : 89–114. [Google Scholar]
- Bestel J, Clément F, Sorine M. A biomechanical model of muscle contraction. In : Niessen WJ, Viergever MA, eds. Lecture notes in computer science, vol. 2208. New York : Springer Verlag, 2001. [Google Scholar]
- Jülicher F, Adjari A, Prost J. Modeling molecular motors. Rev Modern Phys 1997; 69 : 1269–81. [Google Scholar]
- Hill AV. The heat of shortening and the dynamic constants in muscle. Proc Roy Soc Lond B Biol Sci 1938; 126 : 136–95. [Google Scholar]
- Chapelle D, Clément F, Génot F, et al. A physiologically-based model for active cardiac muscle contraction. In : Katila T, Magnin I, Clarysse P, et al. eds. Functional imaging and modeling of the heart. New York : Springer Verlag, 2001. [Google Scholar]
- Blum J, Le Dimet FX. Assimilation de données pour les fluides géophysiques. Matapli 2002; 67 : 33–55. [Google Scholar]
- Sainte-Marie J, Chapelle D, Sorine M. Data assimilation for an electromechanical model of the myocardium. In : Bathe KJ, ed. Proceedings of the second MIT Conference on computational fluid and solid mechanics, 17-20 juin 2003, Cambridge, MA, USA, vol. 2. Amsterdam : Elsevier, 2003. [Google Scholar]
Liste des figures
 |
Figure 1. Propagation d’une onde de pression dans un anévrisme. Les quatre images représentent la pression dans l’anévrisme à des instants différents (bleu : pression faible, orange : pression forte). Le couplage entre l’écoulement du sang et le déplacement de la paroi artérielle est pris en compte : noter que la paroi de l’anévrisme se déforme, ce qui engendre la propagation de l’onde de pression. La géométrie sur laquelle a été effectuée la simulation provient d’une image médicale. Elle a été « maillée » (triangles noirs) pour permettre d’effectuer le calcul. |
| Dans le texte | |
 |
Figure 2. Angle des fibres (cosinus) sur 3 coupes orthogonales. La couleur représente la valeur du cosinus de l’angle que présente au point considéré la fibre avec le plan orthogonal à l’axe principal du cœur. On voit que cet angle est maximal près de l’épicarde et de l’endocarde (source : R. Cimrman, INRIA, Rocquencourt). |
| Dans le texte | |
 |
Figure 3. Vues en coupe des déformations du myocarde en fin de diastole (A) et de systole (B). Les couleurs représentent l’amplitude des déplacements par rapport à la position de fin de diastole (bleu : plus faible, rouge : plus élevée), et les lignes blanches le maillage de calcul (source : J. Sainte-Marie, INRIA, Rocquencourt). |
| Dans le texte | |
 |
Figure 4. Résultat de l’assimilation sur σ0. Les couleurs représentent les valeurs du paramètre (bleu pour une contractilité anormalement faible). Les résultats obtenus par la procédure d’assimilation (B) sont en bonne adéquation avec les valeurs de référence (A) ayant servi à engendrer les données synthétiques (source : J. Sainte-Marie, INRIA, Rocquencourt). |
| Dans le texte | |
Les statistiques affichées correspondent au cumul d'une part des vues des résumés de l'article et d'autre part des vues et téléchargements de l'article plein-texte (PDF, Full-HTML, ePub... selon les formats disponibles) sur la platefome Vision4Press.
Les statistiques sont disponibles avec un délai de 48 à 96 heures et sont mises à jour quotidiennement en semaine.
Le chargement des statistiques peut être long.




