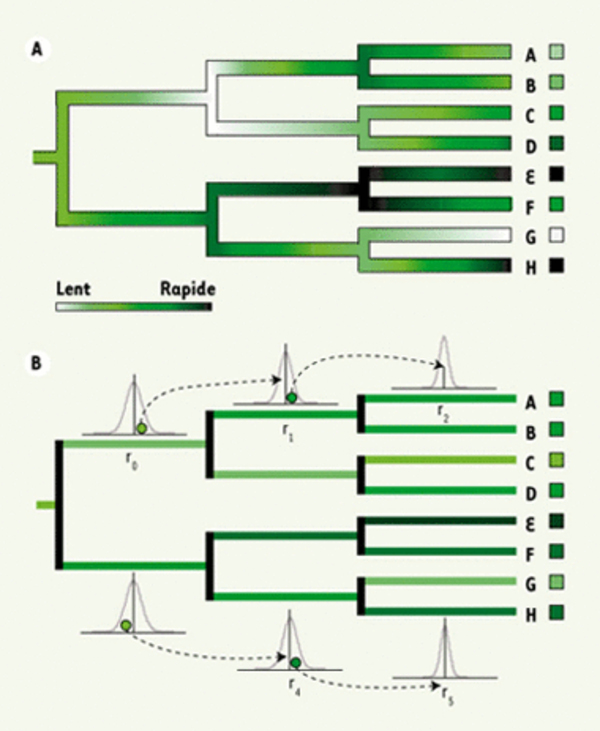
Figure 2.
Télécharger l'image originale
Les horloges moléculaires assouplies. A. Les variations graduelles de taux d’évolution le long des branches d’une phylogénie. À partir de la racine de cette phylogénie, différentes trajectoires conduisent aux taux observés chez les taxons A à H symbolisés dans les carrés correspondants. Les taux d’évolution, de lents jusqu’à rapides, varient le long des branches horizontales. Les branches verticales représentent les événements de spéciation. Ces derniers produisent deux espèces descendantes qui, au moment où elles se séparent l’une de l’autre, possèdent le même taux d’évolution hérité de l’espèce ancestrale dont elles sont issues. Trois principaux cas de figure se présentent ensuite : les espèces accélèrent (C et D), ralentissent (A et B) ou bien l’une accélère (H) tandis que l’autre ralentit (G). Enfin, une espèce peut évoluer de manière quasiment constante, ici rapide (E). B. Le modèle des horloges assouplies avec autocorrélation des taux. Les variations graduelles de taux présentées ci-dessus sont modélisées de la manière suivante. Chaque branche est caractérisée par un unique taux, qui est la moyenne de son taux initial et de son taux final. Le taux r1 d’une branche descendante est tiré (disque vert) dans une distribution normale centrée sur le taux r0 de la branche ascendante. Le taux r1 est ici plus rapide que r0. Les autres relations d’ordre illustrées sont : r2 > r1 > r0, r3 > r4, et r5 > r4. Une variance de cette distribution normale des taux respectivement importante ou faible entraîne un écart important ou faible par rapport à l’hypothèse d’horloge moléculaire.
Les statistiques affichées correspondent au cumul d'une part des vues des résumés de l'article et d'autre part des vues et téléchargements de l'article plein-texte (PDF, Full-HTML, ePub... selon les formats disponibles) sur la platefome Vision4Press.
Les statistiques sont disponibles avec un délai de 48 à 96 heures et sont mises à jour quotidiennement en semaine.
Le chargement des statistiques peut être long.




